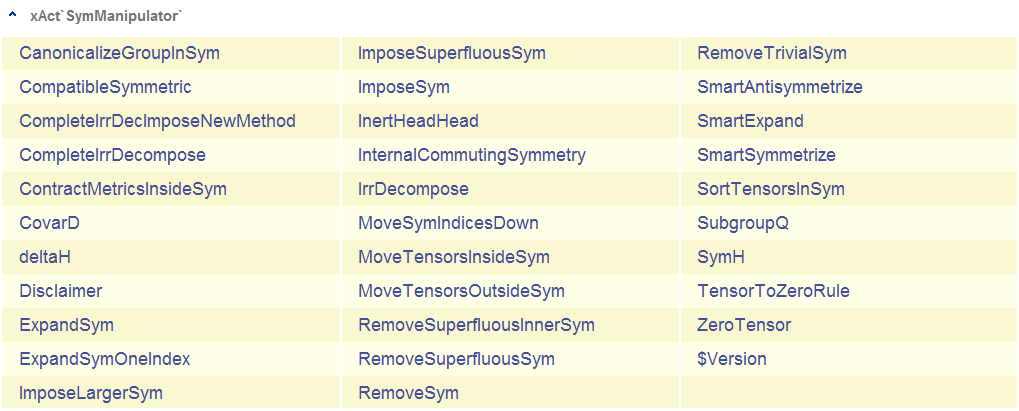
This is the doc file SymManipulatorDoc.nb of version 0.8.3 of SymManipulator`. Last update on 5 May 2012.
Author
© 2011-2012, under the GNU General Public License (GPL)
Thomas Bäckdahl
Max-Planck-Institut für Gravitationsphysik
Albert Einstein Institut
Golm, Germany
thomas.backdahl@aei.mpg.de
Intro
SymManipulator` is the xAct` package for computations with symmetrized tensor expressions. By a symmetrized tensor expression we mean a sum of tensors where each term is the original expression with the indices permuted. We require the set of permutations to form a group. We call this group the imposed symmetry group. It is a group of signed permutations. The sign of the permutation gives the sign of the corresponding term.
Load the package
This loads the package from the default directory, for example $Home/.Mathematica/Applications/xAct/ for a single-user installation under Linux.
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
In[3]:=
<<xAct`TexAct`
![]()
![]()
![]()
![]()

![]()
Comparing, we see that what packages take in Mathematica 8.0:
In[4]:=
![]()
Out[4]=
![]()
In[5]:=
![]()
Out[5]=
![]()
There are several contexts: xAct`SymManipulator`, xAct`xTensor`, xAct`xPerm` and xAct`xCore` contain the respective reserved words. System` contains Mathematica's reserved words. The current context Global` will contain your definitions and right now is empty.
In[6]:=
![]()
Out[6]=
![]()
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
![]()
1. Example session
The package works for all dimensions. At the moment only abstract indices can be used.
Basic examples
Definition of a four dimensional manifold M4:
In[9]:=
![]()
![]()
![]()
For most things we don’t need a metric so we do not need to define one now.
We define a tensor without symmetries:
In[10]:=
![]()
![]()
If we want to completely symmetrize T, we can do it using just xTensor:
In[11]:=
![]()
Out[11]=
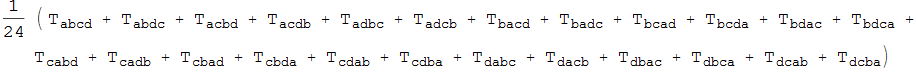
This representation is often inconvenient to use so we can impose the symmetry abstractly instead using ImposeSym:
In[12]:=
![]()
Out[12]=
|
The label (1234) means that the symmetrization is taken over the slots 1, 2, 3 and 4.
We can manipulate this expression, and only expand it when we need to. We expand it with ExpandSym:
In[13]:=
![]()
Out[13]=
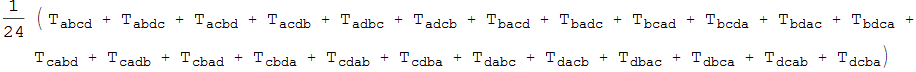
We can check that this is the same as ImposeSymmetry:
In[14]:=
![]()
Out[14]=
![]()
The symmetrized expression is treated as a tensor. That is most xTensor tools will work on it. A new tensor is not defined, so all information is carried in the head of the symmetrized object.
In[15]:=
![]()
Out[15]=
![]()
In[16]:=
![]()
Out[16]=
![]()
In[17]:=
![]()
Out[17]=
![]()
The canonicalizer can therefore work on SymH objects:
In[18]:=
![]()
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
Other groups can also be imposed. For instance symmetrize over -a,-c and antisymmetrize over -b,-d:
In[20]:=
![]()
Out[20]=
|
In[21]:=
![]()
Out[21]=
![]()
If the group has more complicaed structure, the label only shows the slots involved.
In[22]:=
![]()
Out[22]=
|
In[23]:=
![]()
Out[23]=
![]()
TexAct package can produce a nice TeX code output if the symmetrized object is possible to write in a nice way.
In[24]:=
![]()
Out[24]=
|
In[25]:=
![]()
Out[25]=
![]()
In[26]:=
![]()
Out[26]=
|
In[27]:=
![]()
Out[27]=
![]()
The internal tensor can also have symmetries.
In[28]:=
![]()
![]()
In[29]:=
![]()
Out[29]=
|
Now the total symmetry is a mixture of the symmetry of S and the imposed symmetry.
In[30]:=
![]()
Out[30]=
![]()
The calculation of this symmetry has special codes for the cases when the imposed symmetry is the symmetric or antisymmetric group on some indices. In all other cases, a more time consuming code is used to compute the mixed symmetry.
If the tensor already has the the imposed symmetry, it is automatically simplified.
In[31]:=
![]()
Out[31]=
| S |
|
If one antisymmetrizes over a pair of symmetric slots, one will get zero. This idea have been generalized, and this is checked automatically by ImposeSym. This check works for any combination of groups.
In[32]:=
![]()
Out[32]=
![]()
In[33]:=
![]()
Out[33]=
![]()
Sometimes the expansion of a symmetry gives many more terms than need due to the internal symmetry.
In[34]:=
![]()
Out[34]=
|
In[35]:=
![]()
Out[35]=
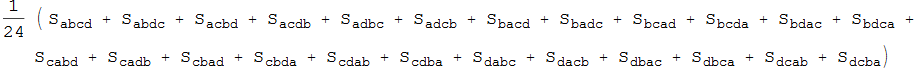
In[36]:=
![]()
Out[36]=
![]()
Then one can give the option SmartExpand->True. Instead of computing all elements of the imposed symmetry group, only a transversal is computed. This is a new feature in release 0.8.3 and not very well tested.
In[37]:=
![]()
Out[37]=
![]()
This idea is used in the new commands SmartSymmetrize and SmartAntisymmetrize. They do the same thing as Symmetrize and Antisymmetrize, but number of terms is reduced by taking the internal symmetry into consideration. Observe that this is a new feature in release 0.8.3 and not very well tested.
In[38]:=
![]()
Out[38]=
![]()
In[39]:=
![]()
Out[39]=
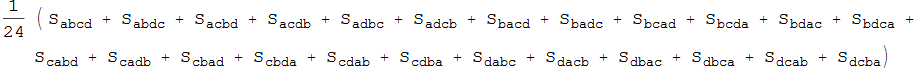
In[40]:=
![]()
Out[40]=
![]()
Product of tensors can be handled. In this case, interchange symmetries etc will be considered as usual.
In[41]:=
![]()
Out[41]=
|
In[42]:=
![]()
Out[42]=
![]()
In[43]:=
![]()
Out[43]=
|
The order of the tensors is automatically sorted by ImposeSym.
In[44]:=
![]()
Out[44]=
|
If one would like to sort them alphabetically at any ther time one can use SortTensorsInSym
In[45]:=
![]()
Out[45]=
|
In[46]:=
![]()
Out[46]=
|
If a tensor is inside the SymH object, but the symmetrization is not acting on its indices, one can move it outside the SymH object.
In[47]:=
![]()
Out[47]=
|
In[48]:=
![]()
Out[48]=
![]()
One can also move tensors inside the SymH object.
In[49]:=
![]()
Out[49]=
|
Symmetrizations can be nested
In[50]:=
![]()
Out[50]=
|
In[51]:=
![]()
Out[51]=
|
ExpandSym only expands the outermost SymH object
In[52]:=
![]()
Out[52]=
![]()
In[53]:=
![]()
Out[53]=
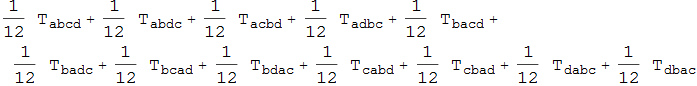
Sometimes, when nesting symmeries the inner symmetrization might not be needed because of the outer symmetrization. Then this can be removed by RemoveSuperfluousInnerSym
In[54]:=
![]()
Out[54]=
|
In[55]:=
![]()
Out[55]=
|
In[56]:=
![]()
Out[56]=
|
In[57]:=
![]()
Out[57]=
![]()
The functions for dealing with nested SymH objects work best when all tensors are innermost. To get that, use MoveTensorsInsideSym before you apply the second ImposeSym.
In[58]:=
![]()
Out[58]=
![]()
In[59]:=
![]()
Out[59]=
|
In[60]:=
![]()
Out[60]=
|
In[61]:=
![]()
Out[61]=
|
In[62]:=
![]()
Out[62]=
|
In[63]:=
![]()
Out[63]=
|
In[64]:=
![]()
Out[64]=
![]()
Examples with a metric
Definition of a Lorentzian metric on the manifold:
In[65]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If you contract indices of a SymH object, this is means that the symmetrization is done first and then the contraction.
In[66]:=
![]()
Out[66]=
|
In[67]:=
![]()
Out[67]=
|
In[68]:=
![]()
Out[68]=
![]()
In[69]:=
![]()
Out[69]=
![]()
Observe that the symmetrization and trace operations do not commute in general as seen by this example:
In[70]:=
![]()
![]()
In[71]:=
![]()
Out[71]=
| V |
|
In[72]:=
![]()
Out[72]=
![]()
In[73]:=
![]()
Out[73]=
![]()
In[74]:=
![]()
Out[74]=
![]()
In[75]:=
![]()
Out[75]=
![]()
In[76]:=
![]()
Out[76]=
![]()
In[77]:=
![]()
Out[77]=
![]()
The same example with SymH objects:
In[78]:=
![]()
Out[78]=
| V |
|
In[79]:=
![]()
Out[79]=
![]()
In[80]:=
![]()
Out[80]=
![]()
In[81]:=
![]()
Out[81]=
|
In[82]:=
![]()
Out[82]=
|
In[83]:=
![]()
Out[83]=
![]()
However, symmetrization and traces do commute if the traces and symmetrizations are taken over disjoint sets of indices.
In[84]:=
![]()
Out[84]=
| V |
|
In[85]:=
![]()
Out[85]=
![]()
In[86]:=
![]()
Out[86]=
![]()
In[87]:=
![]()
Out[87]=
|
In[88]:=
![]()
Out[88]=
|
In[89]:=
![]()
Out[89]=
![]()
In[90]:=
![]()
Out[90]=
![]()
In[91]:=
![]()
Out[91]=
![]()
In[92]:=
![]()
Out[92]=
![]()
Sometimes there is a metric inside the SymH object that later can be contracted. The code for ContractMetricsInsideSym is new in release 0.8.3 and is not well tested.
In[93]:=
![]()
Out[93]=
|
In[94]:=
![]()
Out[94]=
|
In[95]:=
![]()
Out[95]=
|
In[96]:=
![]()
Out[96]=
![]()
Examples with a derivative
This far only derivatives compatible with the metric are handled. Prefix notation is used.
In[97]:=
![]()
Out[97]=
![]()
The derivative index is the first index of the SymH object. That is, we keep the order of the indices when we use prefix notation.
In[98]:=
![]()
Out[98]=
|
In many cases the TexAct package can produce the correct TeX code for the expression.
In[99]:=
![]()
In[100]:=
![]()
Out[100]=
![]()
The derivative is internally represented by CovarD[CD,T,{-TangentM4}]. The list {-TangentM4} gives VBundle for the derivative index.
In[101]:=
![]()
Out[101]//InputForm=
SymH[{CovarD[CD, T, {-TangentM4}]}, StrongGenSet[{1, 2, 4},
GenSet[Cycles[{1, 2}], Cycles[{2, 4}]]], "(124)"][-a,
-b, -c, -d, -f]
Higher order derivatives also work
In[102]:=
![]()
Out[102]=
![]()
In[103]:=
![]()
Out[103]=
|
In[104]:=
![]()
Out[104]=
![]()
Examples with irreducible decompositions of Spinors (new feature)
The IrrDecompose code needs spinors and loads it if it is not already loaded
In[105]:=
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Out[105]=
![]()
Define the spin structure
In[106]:=
![]()
Out[106]=

In[107]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Define some spinors
In[108]:=
![]()
In[109]:=
![]()
In[110]:=
![]()
In[111]:=
![]()
In[112]:=
![]()
In[113]:=
![]()
The basic example is
In[114]:=
![]()
Out[114]=
![]()
It can be tested by making all possible contractions and symmetrizations
In[115]:=
![]()
Out[115]=
![]()
In[116]:=
![]()
Out[116]=
![]()
In[117]:=
![]()
Out[117]=
![]()
A sligthly more complicated case
In[118]:=
![]()
Out[118]=
![]()
The IrrDecompose code uses the symmetries of the expression to simplify it
In[119]:=
![]()
Out[119]=
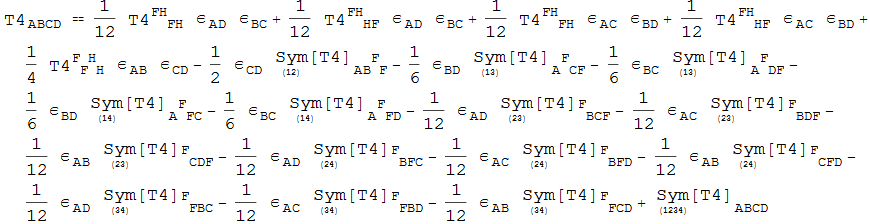
In[120]:=
![]()
Out[120]=
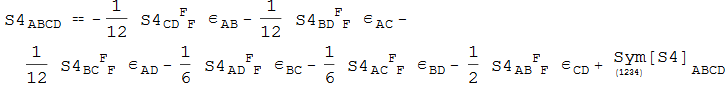
One can also simplify it afterwards
In[121]:=
![]()
Out[121]=
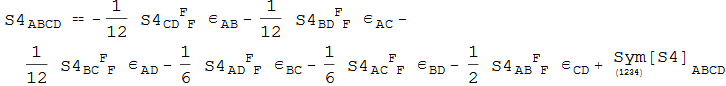
In[122]:=
![]()
Out[122]=
![]()
The decomposition can be simplified further. We see that the left hand side of IrrDecS4 is symmetric in {-A,-B,-C}, but this is not obvoius on the right hand side.
In[123]:=
![]()
Out[123]=
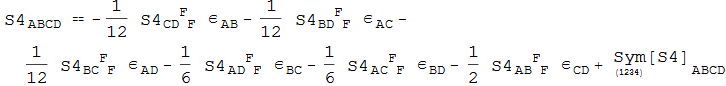
In[124]:=
![]()
Out[124]=
![]()
The function CompleteIrrDecompose automatically finds this symmetry and imposes it
In[125]:=
![]()
![]()
![]()
Out[125]=
![]()
Larger cases can be handled
In[126]:=
![]()
![]()
![]()
Out[126]=
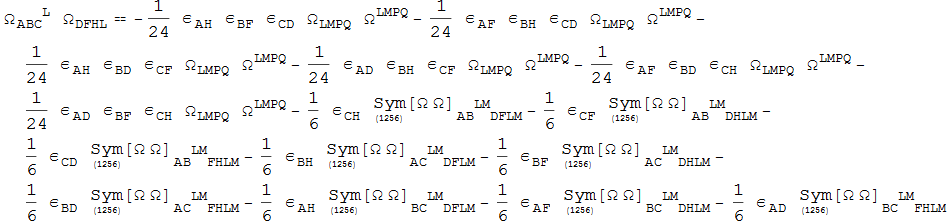
And even larger
In[127]:=
![]()
![]()
![]()
Out[127]=
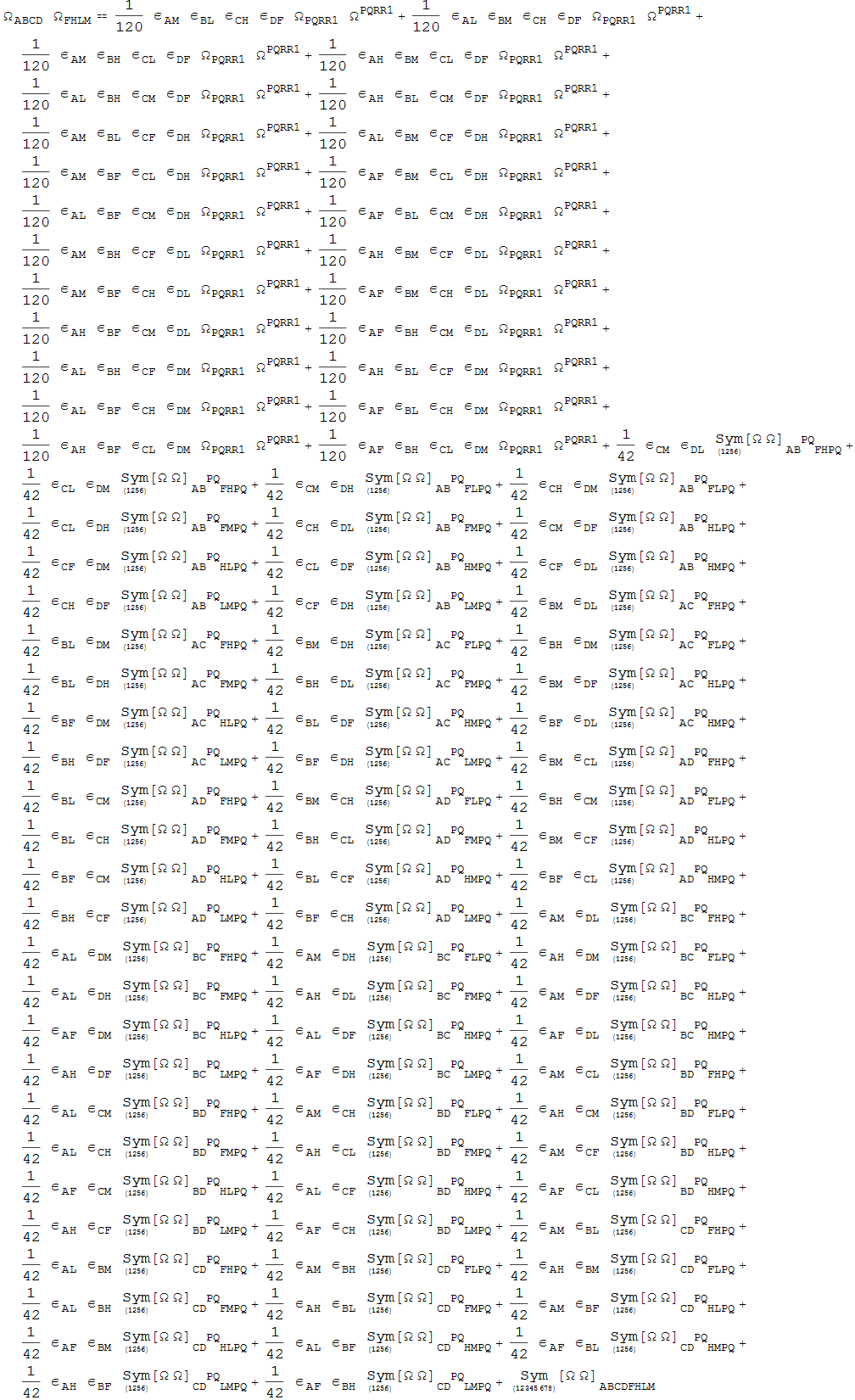
Notes
In[128]:=
![]()
Out[128]=
![]()
In[129]:=
![]()
Out[129]=
![]()
Note: For further information about SymManipulator`, and to be kept informed about new releases, you may contact the author electronically at thomas.backdahl@aei.mpg.de. This is SymManipulatorDoc.nb, the docfile of SymManipulator`, currently in version 0.8.3.
In[130]:=
![]()