7. Manipulation of input
7.1. Symmetry
Every product of tensors or tensorial expressions has a well defined symmetry under permutations of its indices, and this can be obtained with the function SymmetryOf. For convenience, apart from the permutation group describing the symmetry, this function returns the original expression with indices numbered, so that it is clear which indices the permutations are referring to. For example, for a tensor Rie with the symmetries of a Riemann tensor, the symmetry returned by SymmetryOf would be this expression with head Symmetry:
Symmetry[4,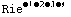
,{●1→G,●2→F,●3→D,●4→K},StrongGenSet[{1,2,3},GenSet[Cycles[{1,3},{2,4}],-Cycles[{1,2}],-Cycles[{3,4}]]]]
The symmetry group is written in strong generating set notation, and its permutations are written in cyclic notation. For explanation of these and other concepts in permutation group theory see the documentation for the companion package xPerm`.
The symmetry of a product of tensors is computed from the symmetries of the individual tensors (stored in SymmetryGroupOfTensor) and taking into account the possibility of permuting equal subexpressions. When there are derivatives involved the computation is more complicated and we need to know whether the derivatives commute, or whether it is possible to permute indices with different characters. The options CommutePDs and ConstantMetric of SymmetryOf help in controlling these points. The global variable $CommuteCovDsOnScalars turns on and off the commutativity of symmetric covariant derivatives on scalar fields.
7.2. Canonicalization and simplification
The main part of a computer algebra system is the canonicalizer, the algorithm in chart of bringing any expression to its canonical form. In xTensor` the canonicalizer is implemented in a single command, called ToCanonical, by far the most sophisticated algorithm of the whole system. Its action is composed of three steps:
1) On a sum of terms we first apply the function SameDummies to minimize the number of different dummy indices. Then we map ToCanonical over individual terms, such that each of them is canonicalized independently.
2) Terms (generically products of different objects) are sorted according to a number of criteria. This is done by the function xSort. This function works in three internal steps, corresponding to three respective internal (private) functions:
2.1) Identify: Dismantle the expression adding symbols characterizing each of its parts
2.2) MarkBlocked: mark those subexpressions with only blocked indices; they do not require canonicalization
2.3) ObjectSort: sorts the different parts of the expression taking into account their properties. The global variable $CommuteFreeIndices controls the ordering of equivalent objects with free indices.
3) Once the term has been sorted, it can be considered as a single tensor with indices and symmetry as given by SymmetryOf. Then we "only" have to call the algorithms for canonicalization of permutations in single and double cosets which have been developed by R. Portugal and his collaborators. These algorithms have been encoded in the companion package xPerm` and constitute the hardest part of the canonicalization process. xPerm` offers two different (but equivalent) encodings of the algorithm: a pure-Mathematica code CanonicalPerm and a mixed-C-Mathematica code MathLinkCanonicalPerm, which is much faster but is not available for all platforms (see the documentation of xPerm` for details). Which of the two is used is chosen through the option MathLink of ToCanonical. (The name of the option comes from the fact the MathLink protocol is used the link the C and Mathematica parts of the code.) By default ToCanonical returns only the canonical expression, but the option GivePerm returns both the canonical expression and the corresponding canonical permutation. The option Notation controls how permutations are handled internally.
Apart from those three (permutation-related), there are three more options for ToCanonical. One of them reports information on the progress of the canonicalization process: Verbose. (There are also the options xPermVerbose and TimeVerbose to get information and timings on the actual permutation-canonicalization process from xPerm`.) Then there is the option UseMetricOnVBundle, which gives a list of vbundles on which the metric can be used to raise and lower the indices. The final issue is that of canonicalization of derivatives: when there is a metric and a derivative which is not compatible with that metric, the system changes to the internal function ToCanonicalDers, which handles canonicalization much more carefully, but also much more slowly. That change can be avoided by switching off the global variable $MixedDers. This new algorithm usually produces lots of Christoffel tensor because it changes internally from the "offending" derivative to the Levi-Civita connection of the metric. It is possible to convert automatically those Christoffel tensors into derivatives of the metric using the option ExpandChristoffel.
Finally, there is the function Simplification, which is simply a combination of ToCanonical and then call to Simplify.
7.3. Imposing symmetries
Given an expression expr and a symmetry group G the function ImposeSymmetry[expr, inds, G] constructs the linear combination of all index-permutations of expr corresponding to the elements of the group G applied on the indices inds of expr, in particular taking expr to be the expression corresponding to the identity element. The result is always divided by the order of G (the number of elements). Special derived functions for special groups of permutations are Symmetrize, Antisymmetrize, PairSymmetrize and PairAntisymmetrize, with obvious meanings.
We can also handle symmetry operations involving a metric: the function STFPart returns the symmetric trace-free part of an expression with respect to a given metric.
More ambitious, but still restricted to the case of a single vbundle, are the functions ChangeFreeIndices, which changes the free abstract indices of an expression to those given by the user, and the function EqualExpressionsQ, which checks whether two expressions are the same apart from symmetries and permutations of indices.
7.4. Collecting terms
There are three simple functions which help in manipulating tensor expressions. These three functions are currently very simple and will be improved in future versions:
IndexCoefficient[expr, form] returns the coefficient of form in expr.
IndexCollect[expr, form, function] imitates the action of Collect but allowing for indexed expressions in form.
IndexSolve[equation, tensor] solves equation for the given tensor in very simple cases: tensor has only free indices
7.5. Acting on particular subexpressions
In xTensor` there are no special functions or arguments to act at particular positions of an expression. This is because Mathematica already offers lots of different possibilities to act on arbitrary positions in different ways. See for example the functions Map, MapAt, MapAll, MapIndexed, etc. However, it is sometimes difficult to know in which position a given subexpression is, and for this an other similar purposes the functions ColorPositionsOfPattern and ColorTerms are really useful. These two have been constructed using the functionality of the great package ExpressionManipulation` by David J.M. Park Jr., Ted Ersek (C) 1999-2007.
