8.2. Riemann expressions
As we said, there is no algorithm at present in xTensor` to canonicalize expressions with multiterm symmetries. That is an obstacle in GR when one wants to work with the Riemann tensor, which has a cyclic symmetry. A simple, brute-force, solution is to prepare a number of rules which are only valid for the Riemann tensor. We follow MathTensor's discussion of this point (see MathTensor book).
There are 48 rules in total, numbered from 1 to 40, some of them having subcases a, b, c, ...
14 of those rules are simple consequences of the monoterm symmetries of the Riemann tensor, and hence can be considered already implemented in ToCanonical:
RiemannRule1:
In[805]:=
![]()
Out[805]=
![]()
In[806]:=
![]()
Out[806]=
![]()
RiemannRule2:
In[807]:=
![]()
Out[807]=
![]()
RiemannRule3:
In[808]:=
![]()
Out[808]=
![]()
RiemannRule4:
In[809]:=
![]()
Out[809]=
![]()
RiemannRule5:
In[810]:=
![]()
Out[810]=
![]()
RiemannRule6:
In[811]:=
![]()
Out[811]=
![]()
In[812]:=
![]()
Out[812]=
![]()
RiemannRule31:
In[813]:=
![]()
Out[813]=
![]()
In[814]:=
![]()
Out[814]=
![]()
RiemannRule32:
In[815]:=
![]()
Out[815]=
![]()
In[816]:=
![]()
Out[816]=
![]()
RiemannRule33:
In[817]:=
![]()
Out[817]=
![]()
In[818]:=
![]()
Out[818]=
![]()
There are 2 more rules which can be obtained from the fact that the Einstein tensor is divergence free:
RiemannRule16:
In[819]:=
![]()
Out[819]=
![]()
RiemannRule17:
In[820]:=
![]()
Out[820]=
![]()
The other 32 rules are actual consequences of the cyclic symmetry of the Riemann tensor, and therefore must be programmed independently. Using MakeRule we can avoid typing equivalent rules (up to permutations of indices), reducing the number to 17 independent rules.
We first study 13 rules having derivatives of a single curvature tensor on the LHS. They are in fact only 6 independent rules:
RuleDivRiemann
RuleDivGradRicci
RuleBoxRiemann
RuleDivGradRiemann
RuleD4RicciScalar
RuleD4Ricci
The four rules 20--23 are all the same:
In[821]:=
![RuleDivRiemann = MakeRule[{CD[a] @ RiemannCD[-a, -b, -c, -d], -CD[-d] @ RicciCD[-b, -c] + CD[-c] @ RicciCD[-b, -d]}, UseSymmetries→True, MetricOn→All] ;](../HTMLFiles/xTensorDoc.nb_2020.gif)
RiemannRule20:
In[822]:=
![]()
Out[822]=
![]()
RiemannRule21:
In[823]:=
![]()
Out[823]=
![]()
RiemannRule22:
In[824]:=
![]()
Out[824]=
![]()
RiemannRule23:
In[825]:=
![]()
Out[825]=
![]()
Two rules with second derivatives of Ricci can be combined in a single rule:
In[826]:=

RiemannRule18:
In[827]:=
![]()
Out[827]=
![]()
RiemannRule19:
In[828]:=
![]()
Out[828]=
![]()
Rules 26 to 30 are now two rules in xTensor`:
In[829]:=

In[830]:=

RiemannRule26:
In[831]:=
![]()
Out[831]=
![]()
RiemannRule27:
In[832]:=
![]()
Out[832]=
![]()
RiemannRule28:
In[833]:=
![]()
Out[833]=
![]()
RiemannRule29:
In[834]:=
![]()
Out[834]=
![]()
RiemannRule30:
In[835]:=
![]()
Out[835]=
![]()
Fourth derivative of the Ricci scalar: conversion to Box^2:
In[836]:=

RiemannRule24:
In[837]:=
![]()
Out[837]=
![]()
Fourth derivative of the Ricci tensor:
In[838]:=

RiemannRule25:
In[839]:=
![]()
Out[839]=
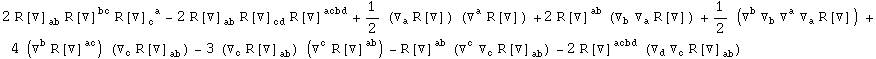
Now we study six rules with products of two Riemann tensors on the LHS. There are only two different rules, depending on whether there are two or three contracted indices:
RuleTwoRiemann3
RuleTwoRiemann2
These are the independent rules:
In[840]:=
![]()
In[841]:=
![]()
RiemannRule7:
In[842]:=
![]()
Out[842]=
![]()
RiemannRule8:
In[843]:=
![]()
Out[843]=
![]()
RiemannRule9a:
In[844]:=
![]()
Out[844]=
![]()
RiemannRule9b:
In[845]:=
![]()
Out[845]=
![]()
RiemannRule9c:
In[846]:=
![]()
Out[846]=
![]()
RiemannRule9d:
In[847]:=
![]()
Out[847]=
![]()
There are seven more rules involving two curvature tensors and derivatives, corresponding to five independent rules:
RuleD01TwoRiemann
RuleD11TwoRiemann
RuleD2RicciRiemann
RuleD2RicciDRiemann
RuleD11bisTwoRiemann
In[848]:=
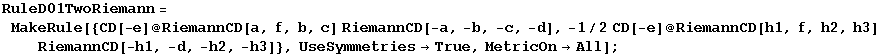
In[849]:=
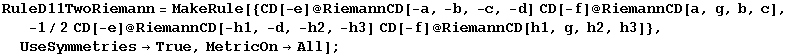
In[850]:=
![]()
In[851]:=

This rule has a typo in MathTensor's book. I assume the index c on the RHS is actually f:
In[852]:=

RiemannRule34:
In[853]:=
![]()
Out[853]=
![]()
RiemannRule35:
In[854]:=
![]()
Out[854]=
![]()
RiemannRule36:
In[855]:=
![]()
Out[855]=
![]()
RiemannRule37:
In[856]:=
![]()
Out[856]=
![]()
RiemannRule38:
In[857]:=
![]()
Out[857]=
![]()
RiemannRule39:
In[858]:=
![]()
Out[858]=
![]()
RiemannRule40:
In[859]:=
![]()
Out[859]=
![]()
Finally we study six rules with products of three curvature tensors, only four of which are independent:
RuleRicciTwoRiemann
RuleThreeRiemann
RuleThreeRiemannB
RuleThreeRiemannC
Constructing the independent rules takes rather long because there are lots of equivalent cases:
In[860]:=
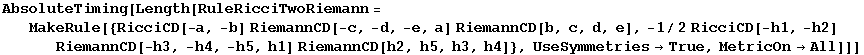
Out[860]=
![]()
In[861]:=
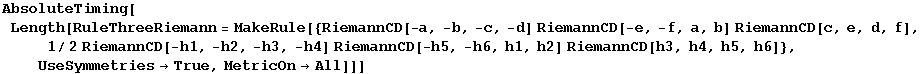
Out[861]=
![]()
In[862]:=
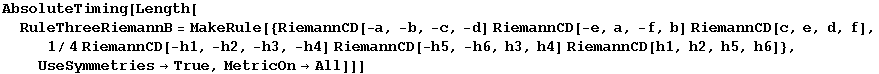
Out[862]=
![]()
In[863]:=
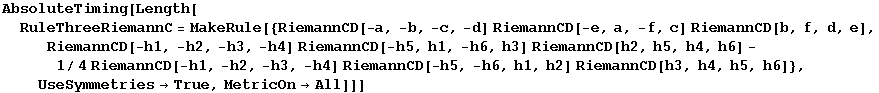
Out[863]=
![]()
RiemannRule10:
In[864]:=
![]()
Out[864]=
![]()
RiemannRule11:
In[865]:=
![]()
Out[865]=
![]()
RiemannRule12:
In[866]:=
![]()
Out[866]=
![]()
RiemannRule13:
In[867]:=
![]()
Out[867]=
![]()
RiemannRule14:
In[868]:=
![]()
Out[868]=
![]()
RiemannRule15:
In[869]:=
![]()
Out[869]=
![]()
| Created by Mathematica (May 16, 2008) |