7.10. Variational derivatives

There is not yet a concept of integration in xTensor`. Instead of working with a variational derivative of a functional, we shall assume that such a functional is the integral of some integrand (or "Lagrangian") and that the integral is computed with respect to a volume form which vanishes under the action of some derivative (this is the derivative which will be "integrated by parts").

Let us fake the presence of a scalar density:

In[761]:=

We need only these two properties:

In[762]:=

In[763]:=

For instance, let us compute the RicciScalar field of our metric:

In[764]:=

Out[764]=

Working intensively with partial derivatives, it is interesting to set

In[765]:=

Out[765]=

Now we perform a direct variational derivative of the Einstein-Hilbert Lagrangian with respect to the inverse metric. It is a long computation, producing 501 terms:

In[766]:=

Out[766]=

The expected result is the Einstein tensor:

In[767]:=

Out[767]=

In[768]:=

Out[768]=

Let us now define the electromagnetic fields:

In[769]:=

In[770]:=

In[771]:=

This is the electromagnetic Lagrangian:

In[772]:=

Out[772]=

and these are the Maxwell equations on a curved background:

In[773]:=

Out[773]=

In[774]:=

Out[774]=

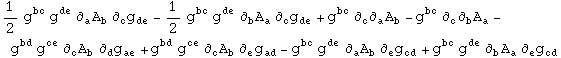
In[775]:=

Out[775]=

In[776]:=

Restore standard options:

In[777]:=

Out[777]=

Created by Mathematica  (May 16, 2008)