7.8. Induced metrics
xTensor` has a simple way to define the induced metric obtained from projection of another metric along hypersurface-orthogonal vector fields, as it is typically done in the ADM 3+1 decomposition of the spacetime metric:
We first define the global ambient metric:
In[632]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Define the timelike normal to the slices. The use of MakeRule and AutomaticRules will be explained later.
In[633]:=
![]()
![]()
In[634]:=
![]()
![]()
In[635]:=
![]()
![]()
We choose the conventions as in Choptuik:
In[636]:=
![]()
![]()
Now we can define the induced metric associated to the pair {ambient metric, orthogonal vector field}. Note that even though there is another metric on the tangent bundle, an induced metric is not considered to be a frozen metric.
In[638]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For a hypersurface orthogonal vector we can express the acceleration vector in terms of a lapse function:
In[639]:=
![]()
![]()
In[640]:=
![]()
Out[640]=
![]()
We define a generic vector field and a spatial vector field:
In[641]:=
![]()
![]()
In[642]:=
![]()
![]()
The first operation we need is the decomposition of any expression along the normal vector. This is given by the command InducedDecomposition, which requires as second argument the pair {projector, normal}. The decomposition process does not change the input; it simply rewrites it in a different way:
Any expression can be decomposed in projected and orthogonal parts with respect to the vector field. Note the special output of the head Projectormetrich:
In[643]:=
![]()
Out[643]=
![]()
In[644]:=
![]()
Out[644]=
![]()
In[645]:=
![]()
Out[645]=
![]()
In[646]:=
![]()
Out[646]=
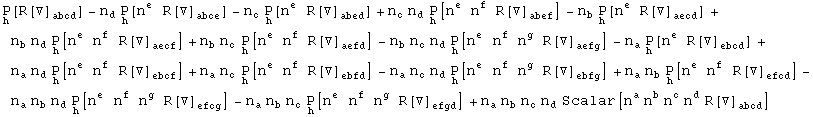
In[647]:=
![]()
Out[647]=
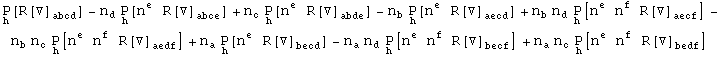
Projection along the normal vector is automatic:
In[648]:=
![]()
Out[648]=
![]()
In[649]:=
![]()
Out[649]=
![]()
In[650]:=
![]()
Out[650]=
![]()
The head Projectormetrich is the formal projector, but we now need a command which actually performs the projection. This is done with ProjectWith[metrich]. Do not confuse them. They have been constructed as a matched pair, and it is very useful to go from the former to the latter.
As long as we need to work only with the projected part of RicciCD, we can use this object:
In[651]:=
![]()
Out[651]=
![]()
However, if we need to perform the projection, we can do this:
In[652]:=
![]()
Out[652]=
![]()
Finally, we can expand the projectors as
In[653]:=
![]()
Out[653]=
![]()
In[654]:=
![]()
Out[654]=
![]()
The projection process can be easily undone using InducedDecomposition:
In[655]:=
![]()
Out[655]=
![]()
InducedDecomposition Decompose an expression along the normal vector
Projector Formal projector head
ProjectWith Actual projection operator, using the projected metric
ProjectorToMetric Convert projected metric into sum of metric and projector onto the normal
MetricToProjector Convert metric into sum of projected metric and projector onto the normal
Projection operators.
The second issue is the manipulation of derivatives. The projected metric has its own Levi-Civita connection, which is a proper covariant derivative only when acting on objects on the projected manifold. The relation between the original and the new covariant derivatives is given by a kind of "Christoffel" encoded in two objects: the extrinsic curvature ExtrinsicK tensor and the Acceleration vector:
This is the derivative of the normal (note the sign convention):
In[656]:=
![]()
Out[656]=
![]()
In[657]:=
![]()
Out[657]=
![]()
It is useful to remove derivatives in favour of these two tensors whenever possible. For example for "spatial" vectors:
In[658]:=
![]()
Out[658]=
![]()
In[659]:=
![]()
Out[659]=
![]()
The opposite command also exists:
In[660]:=
![]()
Out[660]=
![]()
In[661]:=
![]()
Out[661]=
![]()
Let us now project the derivative on a "spatial" vector:
In[662]:=
![]()
Out[662]=
![]()
In[663]:=
![]()
Out[663]=
![]()
In[664]:=
![]()
Out[664]=
![]()
In[665]:=
![]()
Out[665]=
![]()
In[666]:=
![]()
Out[666]=
![]()
In[667]:=
![]()
Out[667]=
![]()
A different way to do it is this:
In[668]:=
![]()
Out[668]=
![]()
In[669]:=
![]()
Out[669]=
![]()
In[670]:=
![]()
Out[670]=
![]()
ExtrinsicK Extrinsic curvature tensor
Acceleration Acceleration vector
GradNormalToExtrinsicK Convert from derivatives of the normal to the extrinsic curvature tensor
ExtrinsicKToGradNormal Convert form the extrinsic curvature tensor to derivatives of the normal
ProjectDerivative Convert derivatives on the projected vbundle into projected derivatives
Induced derivatives.
A very important detail is that of the Leibnitz rule for induced derivatives. It is not valid on expressions not on the projected vbundle!
The vector W lives on the projected vbundle and therefore the Leibnitz rule is valid:
In[671]:=
![]()
Out[671]=
![]()
If there are free non-spatial indices we throw an error message:
In[672]:=
![]()
![]()
With dummy indices we can expand both spatial indices and non-spatial indices:
In[673]:=
![]()
Out[673]=
![]()
In[674]:=
![]()
Out[674]=
![]()
In other cases, we prefer to show a warning and live the expression untouched:
In[675]:=
![]()
![]()
The most important application of this in GR is the ADM-type decomposition of a spacetime. In the rest of this section we reproduce some equations from the well-organized notes on ADM by M. Choptuik.
1) Foliations and normals. We use his same notations for the normal vector and the acceleration vector:
In[676]:=
![]()
Out[676]=
![]()
2) The projection tensor and the spatial metric. We do not follow the sign switch of York. The orthogonal projector is our pair Projectormetrich / ProjectWith[metrich] as explained above.
3) The spatial derivative operator and curvature tensor.
In[677]:=
![]()
Out[677]=
![]()
In[678]:=
![]()
Out[678]=
![]()
In[679]:=
![]()
Out[679]=
![]()
In[680]:=
![]()
Out[680]=
![]()
In[681]:=
![]()
Out[681]=
![]()
The contraction of Ricci into RicciScalar does not work:
In[682]:=
![]()
Out[682]=
![]()
4) The extrinsic curvature tensor
In[683]:=
![]()
Out[683]=
![]()
In[684]:=
![]()
Out[684]=
![]()
In[685]:=
![]()
Out[685]=
![]()
In[686]:=
![]()
Out[686]=
![]()
5) The Gauss-Codazzi equations. Single derivative:
In[687]:=
![]()
![]()
In[688]:=
![]()
![]()
In[689]:=
![]()
Out[689]=
![]()
In[690]:=
![]()
Out[690]=
![]()
In[691]:=
![]()
Out[691]=
![]()
In[692]:=
![]()
Out[692]=
![]()
In[693]:=
![]()
Out[693]=
![]()
In[694]:=
![]()
Out[694]=
![]()
We compare with expression (47) of Choptuik's notes:
In[695]:=
![]()
Out[695]=
![]()
In[696]:=
![]()
Out[696]=
![]()
In[697]:=
![]()
Out[697]=
![]()
Second derivatives. We correct Choptuik's equations (49) and (50), which are missing one term:
In[698]:=
![]()
Out[698]=
![]()
In[699]:=
![]()
Out[699]=
![]()
In[700]:=
![]()
Out[700]=
![]()
In[701]:=
![]()
Out[701]=
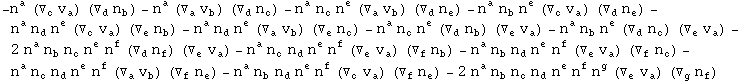
In[702]:=
![]()
Out[702]=
![]()
In[703]:=
![]()
Out[703]=
![]()
In[704]:=
![]()
Out[704]=
![]()
First Gauss-Codazzi equation:
In[705]:=
![]()
Out[705]=
![]()
In[706]:=
![]()
Out[706]=
![]()
In[707]:=
![]()
Out[707]=
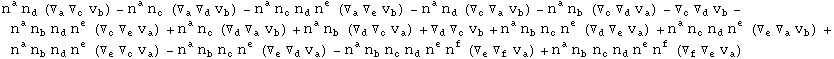
In[708]:=
![]()
Out[708]=
![]()
In[709]:=
![]()
Out[709]=
![]()
In[710]:=
![]()
Out[710]=
![]()
In[711]:=
![]()
Out[711]=
![]()
In[712]:=
![]()
Out[712]=

In[713]:=
![]()
Out[713]=
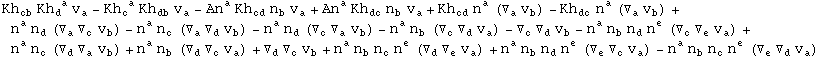
In[714]:=
![]()
Out[714]=
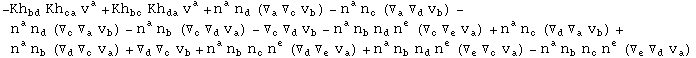
In[715]:=
![]()
Out[715]=
![]()
In[716]:=
![]()
Out[716]=
![]()
If we decompose the Riemann tensor along the vector n
In[717]:=
![]()
Out[717]=

then we can express it as
In[718]:=
![]()
Out[718]=
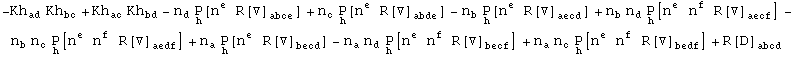
Second Gauss-Codazzi equation:
In[719]:=
![]()
Out[719]=
![]()
In[720]:=
![]()
Out[720]=
![]()
In[721]:=
![]()
Out[721]=
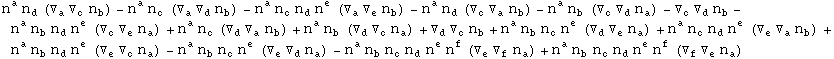
In[722]:=
![]()
Out[722]=
![]()
In[723]:=
![]()
Out[723]=
![]()
In[724]:=
![]()
Out[724]=
![]()
In[725]:=
![]()
Out[725]=
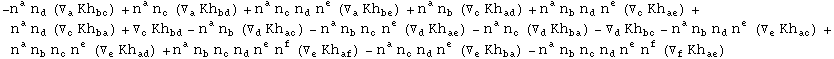
In[726]:=
![]()
Out[726]=
![]()
In[727]:=
![]()
Out[727]=
![]()
We can further decompose the Riemann tensor now:
In[728]:=

Out[728]=
![]()
"Third Gauss-Codazzi equation":
In[729]:=
![]()
Out[729]=
![]()
In[730]:=
![]()
Out[730]=
![]()
In[731]:=
![]()
Out[731]=
![]()
In[732]:=
![]()
Out[732]=
![]()
In[733]:=
![]()
Out[733]=
![]()
In[734]:=
![]()
Out[734]=
![]()
In[735]:=
![]()
Out[735]=
![]()
In[736]:=
![]()
Out[736]=
![]()
Now we have (note that this pair of equations is equivalent to (105) of Choptuik):
In[737]:=
![]()
Out[737]=
![]()
In[738]:=
![]()
Out[738]=
![]()
Finally we can combine the three Gauss-Codazzi equations into a single expression:
In[739]:=

Out[739]=
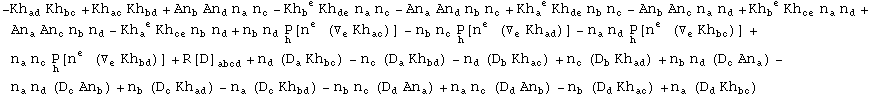
In[740]:=
![]()
Out[740]=
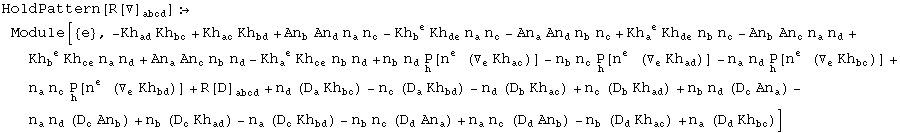
Most of the nontrivial computations in this area can now be easily performed using the Gauss-Codazzi formula. For example, let us compute the projections of the Ricci tensor and the Ricci scalar:
Decompose:
In[741]:=
![]()
Out[741]=
![]()
First formula:
In[742]:=
![]()
Out[742]=
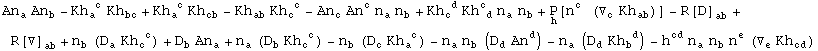
In[743]:=
![]()
Out[743]=
![]()
In[744]:=
![]()
Out[744]=
![]()
In[745]:=
![]()
Out[745]=
![]()
In[746]:=
![]()
Out[746]=
![]()
Second formula:
In[747]:=
![]()
Out[747]=
![]()
In[748]:=
![]()
Out[748]=
![]()
In[749]:=
![]()
Out[749]=
![]()
In[750]:=
![]()
Out[750]=
![]()
In[751]:=
![]()
Out[751]=
![]()
Third formula:
In[752]:=
![]()
Out[752]=
![]()
In[753]:=
![]()
Out[753]=

Finally, the Ricci scalar:
In[754]:=
![]()
Out[754]=
![]()
In[755]:=
![]()
Out[755]=
![]()
In[756]:=
![]()
Out[756]=
![]()
In[757]:=
![]()
Out[757]=
![]()
With a lapse:
In[758]:=
![]()
Out[758]=
![]()
In[759]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[760]:=
![]()
![]()
![]()
| Created by Mathematica (May 16, 2008) |