0.1. Example session

This is a very simple example of the use of xTensor`. We start by defining a manifold and some tensor fields living on its tangent bundle.

Define a 3d manifold M3:

In[10]:=

DefManifold[M3, 3, {a, b, c, d, e}]

** DefManifold: Defining manifold M3.

** DefVBundle: Defining vbundle TangentM3.

Define a contravariant vector v and a covariant antisymmetric tensor F:

In[11]:=

DefTensor[v[a], M3]

DefTensor[F[-a, -b], M3, Antisymmetric[{-a, -b}]]

** DefTensor: Defining tensor v[a] .

** DefTensor: Defining tensor F[-a, -b] .

Tensor product of both tensors, based on the abstract index notation:

In[13]:=

F[-a, -b] v[b]

Out[13]=

F_ab^   v_ ^b

In[14]:=

% v[a]

Out[14]=

F_ab^   v_ ^a v_ ^b

There is no automatic simplification. It must be explicitly asked for:

In[15]:=

Simplification[%]

Out[15]=

0

Example of dummy handling:

In[16]:=

F[-a, -d] v[d] v[b] v[-b] + 3v[b] v[c] v[-c] F[-b, d] F[-d, -a]

Out[16]=

3 F_b ^( d) F_da^   v_ ^b v_c^ v_ ^c + F_ad^   v_b^ v_ ^b v_ ^d

In[17]:=

%//Simplification

Out[17]=

(F_ac^   - 3 F_ad^   F_c ^( d)) v_b^ v_ ^b v_ ^c

There is not a metric and hence v cannot be covariant. Note the position of the head ERROR:

In[18]:=

Validate[%]

Validate :: error : Invalid character of index in tensor F

Validate :: error : Invalid character of index in tensor v

Out[18]=

ERROR[v_b^ ] (F_ac^   - 3 ERROR[F_c ^( d)] F_ad^  ) v_ ^b v_ ^c

Internal structure:

In[19]:=

InputForm[%%]

Out[19]//InputForm=

(F[-a, -c] - 3*F[-a, -d]*F[-c, d])*v[-b]*v[b]*v[c]

Now we define a covariant derivative operator and check the first Bianchi identity (valid for any symmetric connection). Note that xTensor` uses unique (dollar-) variables as internal dummy indices to avoid index collisions. The function ScreenDollarIndices hides those indices replacing them by "normal" indices.

Covariant derivatives are defined by default with curvature but without torsion:

In[20]:=

Options[DefCovD]

Out[20]=

In[21]:=

DefCovD[Cd[-a], {";", "▽"}]

** DefCovD: Defining covariant derivative Cd[-a] .

** DefTensor: Defining vanishing torsion tensor TorsionCd[a, -b, -c] .

** DefTensor: Defining symmetric Christoffel tensor ChristoffelCd[a, -b, -c] .

** DefTensor: Defining Riemann tensor RiemannCd[-a, -b, -c, d] . Antisymmetric only in the first pair.

** DefTensor: Defining non-symmetric Ricci tensor RicciCd[-a, -b] .

** DefCovD:  Contractions of Riemann automatically replaced by Ricci.

In[22]:=

Cd[-a][ F[-b, -c] v[c] ]

Out[22]=

v_ ^c (▽_a^ F_bc^  ) + F_bc^   (▽_a^ v_ ^c)

In[23]:=

%v[b]//Simplification

Out[23]=

F_bc^   v_ ^b (▽_a^ v_ ^c)

The tensors have been defined with their expected symmetries:

In[24]:=

RiemannCd[-a, -b, -c, d] + RiemannCd[-b, -a, -c, d]//Simplification

Out[24]=

0

but it is possible to deduce them from more basic principles:

In[25]:=

RiemannCd[-a, -b, -c, d] + RiemannCd[-b, -a, -c, d]//RiemannToChristoffel//Simplification

Out[25]=

0

In[26]:=

RiemannCd[-a, -b, -c, d] + RiemannCd[-b, -c, -a, d] + RiemannCd[-c, -a, -b, d]//RiemannToChristoffel//Simplification

Out[26]=

0

Check of the second Bianchi identity:

In[27]:=

Antisymmetrize[Cd[-e][RiemannCd[-c, -d, -b, a]], {-c, -d, -e}]

Out[27]=

In[28]:=

3%//Simplification

Out[28]=

▽_c^ R[▽] _deb ^(   a) - ▽_d^ R[▽] _ceb ^(   a) + ▽_e^ R[▽] _cdb ^(   a)

In[29]:=

%//CovDToChristoffel

Out[29]=

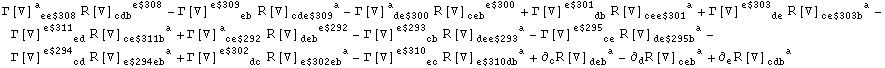
In[30]:=

%//RiemannToChristoffel//ScreenDollarIndices

Out[30]=

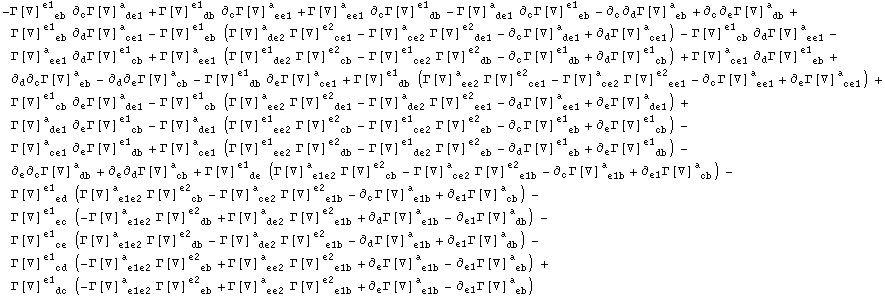
In[31]:=

Simplification[%]//AbsoluteTiming

Out[31]=

{0.282918 Second, 0}

Commutation of covariant derivatives. It is possible to choose the indices (use CommuteCovDs) or just let xTensor` to bring the derivative indices into canonical order (use SortCovDs):

In[32]:=

Cd[-a] @ Cd[-b] @ v[c]

Out[32]=

▽_a^ ▽_b^ v_ ^c

In[33]:=

CommuteCovDs[%, Cd, {-b, -a}]//ScreenDollarIndices

Out[33]=

R[▽] _bad ^(   c) v_ ^d + ▽_b^ ▽_a^ v_ ^c

In[34]:=

SortCovDs[%%]//ScreenDollarIndices

Out[34]=

R[▽] _bad ^(   c) v_ ^d + ▽_b^ ▽_a^ v_ ^c

Now we introduce a metric on the manifold. Its associated curvature tensors are defined: RiemannCD, RiciCD, EinsteinCD, etc:

In[35]:=

DefMetric[-1, g[-a, -b], CD, {"|", "▽"}]

** DefTensor: Defining symmetric metric tensor g[-a, -b] .

** DefTensor: Defining antisymmetric tensor epsilong[a, b, c] .

** DefCovD: Defining covariant derivative CD[-a] .

** DefTensor: Defining vanishing torsion tensor TorsionCD[a, -b, -c] .

** DefTensor: Defining symmetric Christoffel tensor ChristoffelCD[a, -b, -c] .

** DefTensor: Defining Riemann tensor RiemannCD[-a, -b, -c, -d] .

** DefTensor: Defining symmetric Ricci tensor RicciCD[-a, -b] .

** DefCovD:  Contractions of Riemann automatically replaced by Ricci.

** DefTensor: Defining Ricci scalar RicciScalarCD[] .

** DefCovD:  Contractions of Ricci automatically replaced by RicciScalar.

** DefTensor: Defining symmetric Einstein tensor EinsteinCD[-a, -b] .

** DefTensor: Defining vanishing Weyl tensor WeylCD[-a, -b, -c, -d] .

** DefTensor: Defining symmetric TFRicci tensor TFRicciCD[-a, -b] .

   Rules {1, 2} have been declared as DownValues for TFRicciCD .

** DefCovD:  Computing RiemannToWeylRules for dim 3

** DefCovD:  Computing RicciToTFRicci for dim 3

** DefCovD:  Computing RicciToEinsteinRules for dim 3

In[36]:=

CD[-a][ g[-b, -c] ]

Out[36]=

0

In[37]:=

CD[-a][ EinsteinCD[a, b] ]

Out[37]=

0

In[38]:=

g[a, -a]

Out[38]=

3

In[39]:=

g[a, b] g[-b, -c]

Out[39]=

δ_ ( c)^a

Let us check the antisymmetry of the second pair of indices in the Riemann tensor:

In[40]:=

RiemannCD[-a, -b, -c, -d] + RiemannCD[-a, -b, -d, -c]

Out[40]=

R[▽] _abcd^     + R[▽] _abdc^    

Because canonicalization is not automatic, the previous expression is not automatically zero. We expand it in derivatives of Christoffels and canonicalize. The partial derivative does not commute with the metric, so that internally the code replaces temporarily those derivatives with Levi-Civita connections:

In[41]:=

%//RiemannToChristoffel//Simplification//ScreenDollarIndices

ToCanonical :: cmods : Changing derivatives to canonicalize.

ToCanonical :: cmods : Changing derivatives to canonicalize.

ToCanonical :: cmods : Changing derivatives to canonicalize.

General :: stop : Further output of ToCanonical :: cmods will be suppressed during this calculation. More…

Out[41]=

Metric contraction is not automatic either. The resulting expression is not obviously zero:

In[42]:=

%//ContractMetric//Simplification

Out[42]=

Actually it is only zero for connections deriving from a metric:

In[43]:=

%//ChristoffelToGradMetric//Expand

Out[43]=

-1/2 ∂_a^ ∂_b^ g_cd^   - 1/2 ∂_a^ ∂_b^ g_dc^   + 1/2 ∂_b^ ∂_a^ g_cd^   + 1/2 ∂_b^ ∂_a^ g_dc^  

In[44]:=

%//Simplification

Out[44]=

0

In this case a simple reordering of the partial derivatives (this is not automatic) would have been enough:

In[45]:=

%%//SortCovDs

Out[45]=

0

Examples of Lie derivative and bracket:

In[46]:=

LieD[3v[a]][F[-a, -b] v[b]]

Out[46]=

3 v_ ^b (ℒ_vF_ab^  ) + 3 F_ab^   (ℒ_vv_ ^b)

In[47]:=

Bracket[a][v[a], F[a, -b] v[b]]

Out[47]=

[v_ ^a, F_ ( b)^a v_ ^b]^a

Undefine all objects on the manifold and the manifold itself:

In[48]:=

UndefMetric[g]

** UndefTensor: Undefined antisymmetric tensor epsilong

** UndefTensor: Undefined symmetric Christoffel tensor ChristoffelCD

** UndefTensor: Undefined symmetric Einstein tensor EinsteinCD

** UndefTensor: Undefined symmetric Ricci tensor RicciCD

** UndefTensor: Undefined Ricci scalar RicciScalarCD

** UndefTensor: Undefined Riemann tensor RiemannCD

** UndefTensor: Undefined symmetric TFRicci tensor TFRicciCD

** UndefTensor: Undefined vanishing torsion tensor TorsionCD

** UndefTensor: Undefined vanishing Weyl tensor WeylCD

** UndefCovD: Undefined covariant derivative CD

** UndefTensor: Undefined symmetric metric tensor g

In[49]:=

UndefTensor/@{v, F} ;

UndefCovD[Cd]

** UndefTensor: Undefined tensor v

** UndefTensor: Undefined tensor F

** UndefTensor: Undefined symmetric Christoffel tensor ChristoffelCd

** UndefTensor: Undefined non-symmetric Ricci tensor RicciCd

** UndefTensor: Undefined Riemann tensor RiemannCd

** UndefTensor: Undefined vanishing torsion tensor TorsionCd

** UndefCovD: Undefined covariant derivative Cd

In[51]:=

UndefManifold[M3]

** UndefVBundle: Undefined vbundle TangentM3

** UndefManifold: Undefined manifold M3

There are no symbols left in the Global` context

In[52]:=

? Global`*

Information :: nomatch : No symbol matching Global`* found. More…

Created by Mathematica  (May 16, 2008) Valid XHTML 1.1!