3.8. Complex conjugation

Complex conjugation is performed by the function Dagger, except on indices, where we shall use the variant DaggerIndex, to avoid overloading Dagger too much.

Dagger                Complex conjugation of tensor expressions
DaggerIndex            Complex conjugation of indices
DaggerQ                Check for complex objects
TransposeDagger        Transposition of indices of complex conjugate vbundles
$DaggerCharacter    Character which denotes complex conjugates of other objects

Complex conjugation

A tensor with indices on a complex vbundle always has a dagger pair:

In[186]:=

$Tensors

Out[186]=

{T, v, r, TT, Force, S, U}

In[187]:=

DefTensor[V[a, ], TangentM3, Dagger→Complex]

** DefTensor: Defining tensor V[a, ] .

** DefTensor: Defining tensor V†[a, †] .

In[188]:=

? V

Global`V

Dagger[V]^=V†
DependenciesOfTensor[V]^={M3}
Info[V]^={tensor,}
PrintAs[V]^=V
ServantsOf[V]^={V†}
SlotsOfTensor[V]^={TangentM3,InnerC}
SymmetryGroupOfTensor[V]^=StrongGenSet[{},GenSet[]]
TensorID[V]^={}
xTensorQ[V]^=True

In[189]:=

? V†

Global`V†

Dagger[V†]^=V
DependenciesOfTensor[V†]^={M3}
Info[V†]^={tensor,}
MasterOf[V†]^=V
PrintAs[V†]^=V†
SlotsOfTensor[V†]^={TangentM3,InnerC†}
SymmetryGroupOfTensor[V†]^=StrongGenSet[{},GenSet[]]
TensorID[V†]^={}
xTensorQ[V†]^=True

Complex conjugation acts on the name of the tensor and on its indices as well:

In[190]:=

Dagger[ V[a, ℭ] ]

Out[190]=

V†_   ^aℭ†

In[191]:=

UndefTensor[V]

** UndefTensor: Undefined tensor V†

** UndefTensor: Undefined tensor V

Conjugation of indices (this should be used only for programming):

In[192]:=

DaggerIndex/@{a, -b, , -†}

Out[192]=

{a, -b, †, -}

Tensors can be defined with different properties against complex conjugation.

On real vbundles tensors are real by default:

In[193]:=

Options[DefTensor]

Out[193]=

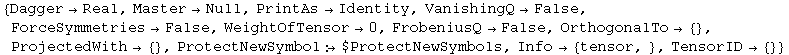
In[194]:=

DefTensor[V[a], M3]

** DefTensor: Defining tensor V[a] .

In[195]:=

Dagger[3I V[a]]

Out[195]=

-3  V_ ^a

In[196]:=

UndefTensor[V]

** UndefTensor: Undefined tensor V

However, it is possible to "complexify" a real vbundle, in such a way that we duplicate its real dimension. Then vectors can have nontrivial complex conjugates:

In[197]:=

DefTensor[V[a], M3, Dagger→Complex]

** DefTensor: Defining tensor V[a] .

** DefTensor: Defining tensor V†[a] .

In[198]:=

Dagger[3I V[a]]

Out[198]=

-3  V†_ ^a

In[199]:=

UndefTensor[V]

** UndefTensor: Undefined tensor V†

** UndefTensor: Undefined tensor V

If the vbundle is complex then all tensors on it must be complex:

In[200]:=

Catch @ DefTensor[V[], M3]

DefTensor :: invalid : Real is not a valid value for Dagger: complex indices .

In[201]:=

DefTensor[V[], M3, Dagger→Complex]

** DefTensor: Defining tensor V[] .

** DefTensor: Defining tensor V†[†] .

In[202]:=

Dagger[3I V[]]

Out[202]=

-3  V†_  ^†

In[203]:=

UndefTensor[V]

** UndefTensor: Undefined tensor V†

** UndefTensor: Undefined tensor V

On complex vbundles it is possible to define Hermitian tensors if they have equal number of indices on both conjugated vbundles (though there is no built-in operation of Hermitian conjugation):

In[204]:=

DefTensor[V[, , ℭ†, †], M3, Dagger→Hermitian]

** DefTensor: Defining tensor V[, , ℭ†, †] .

** DefTensor: Defining tensor V†[†, †, ℭ, ] .

In[205]:=

Dagger[V[, , ℭ†, †]]

Out[205]=

V_      ^ℭ††

In[206]:=

Dagger[V†[†, †, ℭ, ]]

Out[206]=

V_      ^ℭ††

In[207]:=

Catch @ DefTensor[W[, , ℭ†], M3, Dagger→Hermitian]

TransposeDagger :: error : Different number of indices of InnerC and its conjugate InnerC†.

In[208]:=

UndefTensor[V] ;

** UndefTensor: Undefined tensor V†

** UndefTensor: Undefined tensor V

Note that the transposition involved for Hermitian objects does not require any particular ordering of indices of the tensors. However it follows the convention of exchanging the first slot of a given complex vbundle with the first slot of its complex conjugate:

In[209]:=

DefTensor[V[, , ℭ†, †, , †], M3, Dagger→Hermitian]

** DefTensor: Defining tensor V[, , ℭ†, †, , †] .

** DefTensor: Defining tensor V†[†, †, ℭ, , †, ] .

In[210]:=

Dagger[V[, , ℭ†, †, , †]]

Out[210]=

V_         ^ℭ†††

In[211]:=

UndefTensor[V]

** UndefTensor: Undefined tensor V†

** UndefTensor: Undefined tensor V

The symbol for conjugation can be changed using the global variable $DaggerCharacter, but of course the command for complex conjugation will still be called Dagger.

In[212]:=

$DaggerCharacter

Out[212]=

†

Created by Mathematica  (May 16, 2008) Valid XHTML 1.1!