5. Stabilization and Strong Generating Sets
A second essential tool to analyze a group of permutations is the concept of stability.
Given a permutation, there can be points that are not moved:
In[103]:=
![]()
Out[103]=
![]()
Of course, points over the degree of the permutation are not moved:
In[104]:=
![]()
Out[104]=
![]()
Given a generating set GS and a list of points, we call pointwise stabilizer of those points to the subset of GS such that none of the permutations in the subset moves none of the points in the list:
In[105]:=
![]()
Out[105]=
![]()
There is a different concept, that of set-stabilization, requiring that points do not leave the set, though they can move:
In[106]:=
![]()
Out[106]=
![]()
The stabilizer of a group S is a subgroup. However, the stabilizer of a generating set of S is not necessarily a generating set of the subgroup. To solve that problem, Sims introduced the concept of strong generating set: we give a pair formed by a list of points B={![]() , ...,
, ..., ![]() } (called "base") and a generating set GS of the group. The generating set is strong with respect to that base if 1) the stabilizer S(
} (called "base") and a generating set GS of the group. The generating set is strong with respect to that base if 1) the stabilizer S(![]() ,...,
,...,![]() ) of any sorted sublist {
) of any sorted sublist {![]() , ...,
, ..., ![]() }, with m≤k, can be generated by a subset of the permutations in GS, and 2) no permutation in GS fixes all points in the base. The order of points in the base is relevant. This allows us to form a hierarchy of subgroups: S = S() ⊇ S(
}, with m≤k, can be generated by a subset of the permutations in GS, and 2) no permutation in GS fixes all points in the base. The order of points in the base is relevant. This allows us to form a hierarchy of subgroups: S = S() ⊇ S(![]() ) ⊇ S(
) ⊇ S(![]() ,
,![]() ) ⊇ ... ⊇ S(
) ⊇ ... ⊇ S(![]() ,...,
,...,![]() ) = {ID}.
) = {ID}.
Hierarchy of subgroups associated to a simple strong generating set:
In[107]:=
![]()
Out[107]=
| StrongGenSet[{1,3},GenSet[Perm[{2,1,3,4}],Perm[{1,2,4,3}],Perm[{3,4,1,2}]]] |
| StrongGenSet[{3},GenSet[Perm[{1,2,4,3}]]] |
| StrongGenSet[{},GenSet[]] |
Strong generating sets can be calculated from a generating set using the Schreier-Sims algorithm. Example taken from Butler's book:
In[108]:=
![]()
![]()
![]()
In[111]:=
![]()
In[112]:=
![]()
![]()
Out[112]=
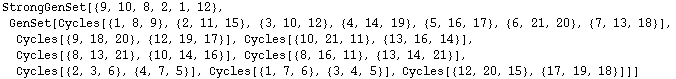
We can give several initial points of the base. Using MathLink is faster, but always returns the result in Images notation:
In[113]:=
![]()
![]()
Out[113]=
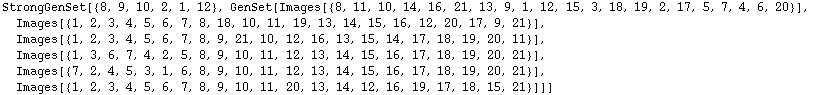
We can also change the base points of a given SGS. This typically introduces many redundant generators and additional points in the base:
In[114]:=
![]()
Out[114]=

In[115]:=
![]()
Out[115]=

Once we have the SGS we can solve any question related to the group:
In[116]:=
![]()
Out[116]=
| StrongGenSet[{9,10,8,2,1,12},GenSet[Cycles[{1,8,9},{2,11,15},{3,10,12},{4,14,19},{5,16,17},{6,21,20},{7,13,18}],Cycles[{9,18,20},{12,19,17}],Cycles[{10,21,11},{13,16,14}],Cycles[{8,13,21},{10,14,16}],Cycles[{8,16,11},{13,14,21}],Cycles[{2,3,6},{4,7,5}],Cycles[{1,7,6},{3,4,5}],Cycles[{12,20,15},{17,19,18}]]] |
| StrongGenSet[{10,8,2,1,12},GenSet[Cycles[{10,21,11},{13,16,14}],Cycles[{8,13,21},{10,14,16}],Cycles[{8,16,11},{13,14,21}],Cycles[{2,3,6},{4,7,5}],Cycles[{1,7,6},{3,4,5}],Cycles[{12,20,15},{17,19,18}]]] |
| StrongGenSet[{8,2,1,12},GenSet[Cycles[{8,16,11},{13,14,21}],Cycles[{2,3,6},{4,7,5}],Cycles[{1,7,6},{3,4,5}],Cycles[{12,20,15},{17,19,18}]]] |
| StrongGenSet[{2,1,12},GenSet[Cycles[{2,3,6},{4,7,5}],Cycles[{1,7,6},{3,4,5}],Cycles[{12,20,15},{17,19,18}]]] |
| StrongGenSet[{1,12},GenSet[Cycles[{1,7,6},{3,4,5}],Cycles[{12,20,15},{17,19,18}]]] |
| StrongGenSet[{12},GenSet[Cycles[{12,20,15},{17,19,18}]]] |
| StrongGenSet[{},GenSet[]] |
In[117]:=
![]()
Out[117]=
![]()
In[118]:=
![]()
Out[118]=
![]()
In[119]:=
![]()
Out[119]=
![]()
A permutation in the group can be uniquely decomposed according to the chain of stabilizers:
In[120]:=
![]()
Out[120]=
![]()
In[121]:=
![]()
Out[121]=
![]()
In[122]:=
![]()
Out[122]=
![]()
or identified from its base images:
In[123]:=
![]()
Out[123]=
![]()
In[124]:=
![]()
Out[124]=
![]()
Not every list of images defines a permutation:
In[125]:=
![]()
![]()
As we said, there is a one to one correspondence between base images and permutations in a group:
In[126]:=
![]()
Out[126]=
| {1,3}→ID |
| {1,4}→-Cycles[{3,4}] |
| {2,3}→-Cycles[{1,2}] |
| {2,4}→Cycles[{1,2},{3,4}] |
| {3,1}→Cycles[{1,3},{2,4}] |
| {3,2}→-Cycles[{1,3,2,4}] |
| {4,1}→-Cycles[{1,4,2,3}] |
| {4,2}→Cycles[{1,4},{2,3}] |
StablePoints Points that are not moved by a permutation
NonStablePoints Construct a base for a group
Stabilizer Subset of permutations that do not move a list of points
SetStabilizer Subset of permutations that do not move a list of points within a set
StabilizerChain Chain of stabilizers of a Strong Generating Set
StrongGenSet Head for a Strong Generating Set
SchreierSims Algorithm to compute a SGS from a GS
BaseChange Change base of a SGS
DeleteRedundantGenerators Drop unnecessary permutations in a SGS
JoinSGS Form SGS for product group
OrderOfGroup Compute order of group described by a SGS
PermMemberQ Check whether a permutation belongs to a group described by a SGS
PermWord Decompose a permutation as a unique product of coset representatives in a SGS hierarchy
FromBaseImage Construct the unique permutation associated to a list of base images
AllBaseImages List all possible base images and their corresponding permutations
Strong Generating Sets.
The main idea behind the Schreier-Sims algorithm is that of "backtrack search". Using the one-to-one mapping between permutations and base images, it is possible to organize all permutations in a group in a tree whose nodes are the possible images of the points in the base. The Schreier vectors allow us to traverse the tree up and down, and the identification between cosets and points of orbits allows us to discard all leaves of the tree below a given node by testing just a single leave. See Butler's book for full details.
The function Search implements backtracking to search for a SGS of a subgroup of a given group:
In[127]:=
![]()
For instance, let us suppose we start from the group ![]() .
.
In[128]:=
![]()
and we want to find a sgs for the subgroup of permutations commuting with permutation z (the so-called centralizer of z):
In[129]:=
![]()
We define the property P identifying the permutations commuting with z:
In[130]:=
![]()
In[131]:=
![]()
Out[131]=
![]()
In[132]:=
![]()
Out[132]=
![]()
The first stabilizer in the chain coincides with the group itself and so we search for the first stabilizer of the subgroup of SGS obeying property P:
In[133]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[133]=
![]()
We see that we have tested 8 permutations in a group of order 24. Only 2 of those 8 form the final sgs of the centralizer, which has order 8:
In[134]:=
![]()
Out[134]=
![]()
Clean up:
In[135]:=
![]()
Search Compute subgroup of permutations obeying a given property
Search subgroups.
| Created by Mathematica (May 16, 2008) |