7.3. Other groups

These are groups taken from the Atlas of Finite Group Representations (http://for.mat.bham.ac.uk/atlas/), in the section Miscellaneous Groups.

This is the exceptional twisted group Sz8 (the Suzuki group), which can be given in terms of permutations on 65 points.

In[241]:=

In[243]:=

Out[243]=

In[244]:=

In[245]:=

Out[245]=

In[246]:=

Out[246]=

This is the exceptional untwisted group G2(4), which can be given in terms of permutations on 416 points.

In[247]:=

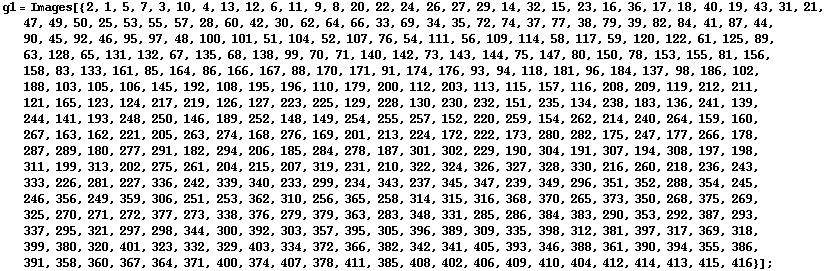
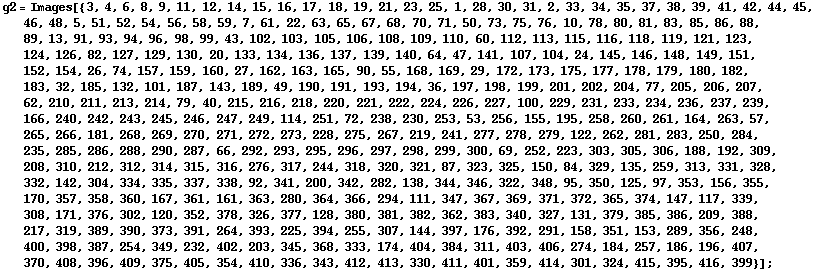
In[249]:=

Out[249]=

In[250]:=

In[251]:=

Out[251]=

In[252]:=

Out[252]=

The largest symplectic group given in the Atlas is S10. It can be represented using permutations of 496 points.

In[253]:=

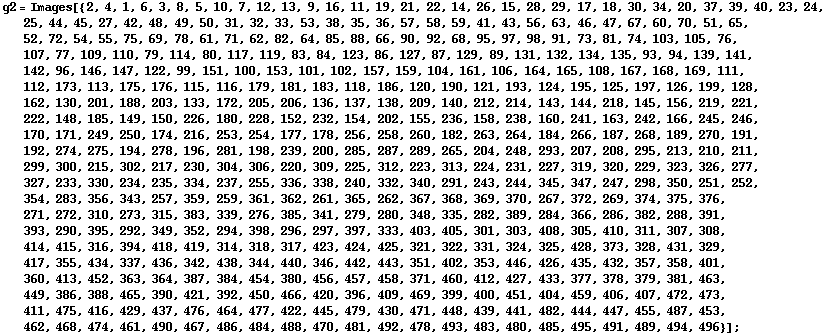
In[255]:=

Out[255]=

In[256]:=

In[257]:=

Out[257]=

In[258]:=

Out[258]=

This is the exceptional twisted group T3D4, represented with permutations on 819 points.

In[259]:=

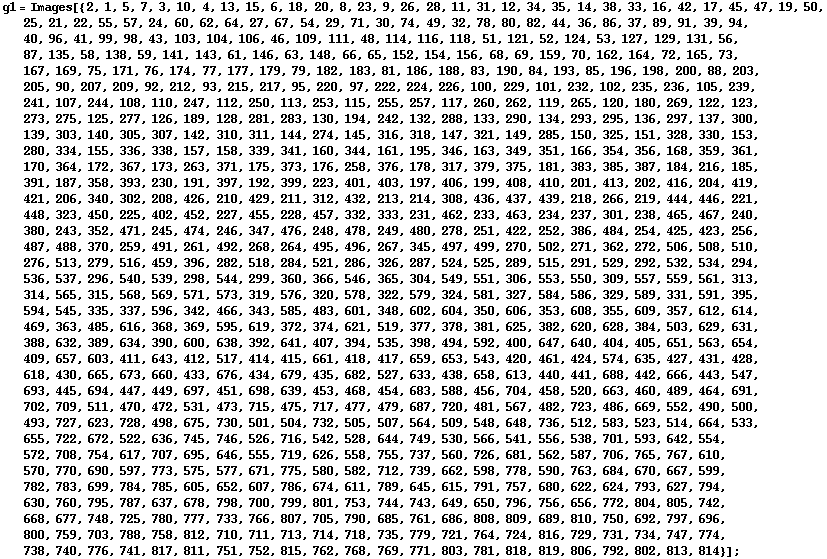
In[261]:=

Out[261]=

In[262]:=

In[263]:=

Out[263]=

In[264]:=

Out[264]=

Go back to the original settings:

In[265]:=

Created by Mathematica  (May 16, 2008)