7.2. Some "small" sporadic simple groups
As further examples of manipulation of nontrivial finite groups, here you find the construction of strong generating sets for some of the 26 sporadic simple groups:
M24 is the largest of the five sporadic simple Mathieu groups, with a permutation representation of degree 24. It was found by Mathieu in 1873. Frobenious showed that the other four simple Mathieu groups (M11, M12, M22, M23) are subgroups of M24.
In[202]:=
![]()
![]()
In[204]:=
![]()
Out[204]=
![]()
In[205]:=
![]()
![]()
In[206]:=
![]()
Out[206]=
![]()
In[207]:=
![]()
Out[207]=
![]()
The sixth sporadic simple group was discovered by Z. Janko in 1965 and it is called Janko1. It can be given in terms of a permutation representation of degree 266:
In[208]:=


In[210]:=
![]()
Out[210]=
![]()
In[211]:=
![]()
![]()
In[212]:=
![]()
Out[212]=
![]()
In[213]:=
![]()
Out[213]=
![]()
The Janko2 group can be given in terms of a permutation representation of degree 100:
In[214]:=
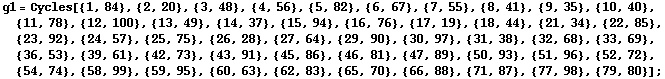
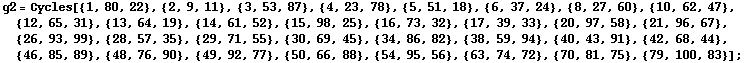
In[216]:=
![]()
Out[216]=
![]()
In[217]:=
![]()
![]()
In[218]:=
![]()
Out[218]=
![]()
In[219]:=
![]()
Out[219]=
![]()
This is the smallest of the three sporadic simple Conway groups, with a permutation representation of degree 276:
In[220]:=


In[222]:=
![]()
Out[222]=
![]()
In[223]:=
![]()
![]()
In[224]:=
![]()
Out[224]=
![]()
In[225]:=
![]()
Out[225]=
![]()
xPerm` can also handle bigger sporadic groups, but it takes very long, or much memory:
This is the smallest of the four sporadic simple Fischer groups. It can be given in terms of a permutation representation of degree 3510. The computation of a SGS requires 400 Mbyte RAM. (The SchreierSims command is deactivated; we read the result from a file.)
In[226]:=
![]()
![]()
In[228]:=
![]()
Out[228]=
![]()
In[228]:=
![]()
![]()
In[230]:=
![]()
![]()
![]()
In[233]:=
![]()
Out[233]=
![]()
In[234]:=
![]()
Out[234]=
![]()
The Janko3 group can be given in terms of a permutation representation of degree 6156. This computation requires almost 900 Mbyte of memory:
In[235]:=
![]()
![]()
In[237]:=
![]()
Out[237]=
![]()
In[238]:=
![]()
![]()
In[239]:=
![]()
Out[239]=
![]()
In[240]:=
![]()
Out[240]=
![]()
| Created by Mathematica (May 16, 2008) |