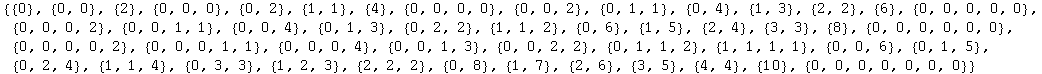2. General concepts and definitions
The Riemann tensor obeys two types of symmetries. The first type are permutation (or monoterm) symmetries, for example,
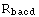 = -
= -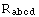 and
and 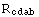 =
= 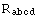 .
.
The second type is the cyclic (or multiterm) symmetry:
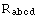 +
+ 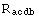 +
+ 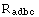 = 0 .
= 0 .
In order to simplify any polynomial of the Riemann tensor, it is necessary to use both kinds. It is possible to use efficient algorithms of computational group theory to manipulate the former, but there are no known efficient algorithms to manipulate the latter.
If we include covariant derivatives, we have to consider two new classes of relations. We have the Bianchi identity:
![R_ab[cd ; e]](../HTMLFiles/InvarDoc.nb_178.gif) =0
=0
and the effect of non commutatity of covariant derivatives:
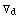
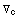
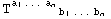 -
- 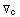
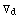
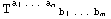 =
=![Underoverscript[∑, k = 1, arg3]](../HTMLFiles/InvarDoc.nb_185.gif)
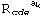
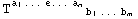 -
-![Underoverscript[∑, k = 1, arg3]](../HTMLFiles/InvarDoc.nb_188.gif)
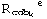
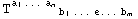
An additional problem is that there are more identities to consider, coming from the fact that some of the polynomial invariants are zero in low-enough dimension. It is possible to show that all these dimension dependent identities are of Lovelock type, that is, they all come from the idea that, on a manifold of dimension dim, antisymmetrizing in dim + 1 indices gives zero. Unfortunately, these last three types of identities cannot be manipulated efficiently either.
The main idea behind Invar` is using the fast canonicalizers of xTensor` and Canon to deal with the permutation symmetries, and then using prestored files of solutions for the other types of identities.
The package is structured as follows:
1. We shall work with two types of invariants:
- (non-dual) invariants: fully contracted products of n Riemann tensors (where n will be called the degree of the invariant), possibly including covariant derivatives .
- dual invariants: fully contracted products of n Riemann tensors with or without derivatives and one epsilon tensor (n is again called the degree of the dual invariant). There is no need to work with more than one epsilon, because products of two epsilons can be converted into delta tensors.
We shall separate the set of all monomial invariants of degree n in subsets  , where
, where 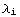 is the differentiation order of the i-th Riemann tensor, assuming the tensors have sorted such that
is the differentiation order of the i-th Riemann tensor, assuming the tensors have sorted such that 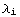 ≤
≤ 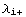 . An n-tuple {
. An n-tuple {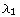 , ...,
, ..., 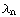 } will be referred to as a case, with the corresponding invariants having N = 4n +
} will be referred to as a case, with the corresponding invariants having N = 4n +![Underoverscript[∑, i = 1, arg3]](../HTMLFiles/InvarDoc.nb_197.gif)
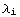 indices and order Λ = 2n +
indices and order Λ = 2n + ![Underoverscript[∑, i = 1, arg3]](../HTMLFiles/InvarDoc.nb_199.gif)
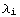 . Λ is the number of derivatives of the metric, not to be confused with the total number of derivatives of the Riemann tensors (the sum of the
. Λ is the number of derivatives of the metric, not to be confused with the total number of derivatives of the Riemann tensors (the sum of the 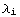 's). Both N and Λ are always even numbers because we only consider scalar expressions. For example, an invariant of the case {0,1,3}, hence with N = 16 indices and order Λ = 10, is
's). Both N and Λ are always even numbers because we only consider scalar expressions. For example, an invariant of the case {0,1,3}, hence with N = 16 indices and order Λ = 10, is
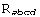
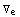

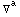
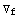
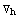
 .
.
2. We shall distinguish six steps or levels of simplification:
1.- Canonicalization with respect to permutation symmetries.
2.- Canonicalization with respect to the cyclic symmetry.
3.- Canonicalization with respect to the Bianchi symmetry.
4.- Canonicalization with respect to commutation of derivatives.
5.- Use of all possible dimensionally-dependent identities.
6.- Conversion of invariants into products of two dual invariants (metric-signature dependent).
3. Each Riemann monomial can be represented in one of three forms (examples will be given below):
- As an explicit tensor expression.
- As a permutation of the indices in canonical order.
- As an expression RInv[metric][case, index] or DualRInv[metric][case, index] which represents the equivalent canonical monomial after canonicalization with respect to the permutation symmetries. The integer index identifies each particular invariant in the list of invariants, sorted according to some predefined ordering.
4. Commands are given to change among those three representations, and to simplify the invariants up to some particular level. They are all listed below. Their mutual structure is schematically given by
In[47]:=
In[48]:=
![SetOptions[Arrow, HeadLength→0.02] ;](../HTMLFiles/InvarDoc.nb_210.gif)

![[Graphics:../HTMLFiles/InvarDoc.nb_213.gif]](../HTMLFiles/InvarDoc.nb_213.gif)
Out[50]=
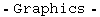
Invar` currently handles invariants up to and including Λ = 12, plus the single case {0, 0, 0, 0, 0, 0, 0} of order 14. The full list of cases can be generated with the following command,
In[51]:=
![InvarCases[]](../HTMLFiles/InvarDoc.nb_215.gif)
Out[51]=
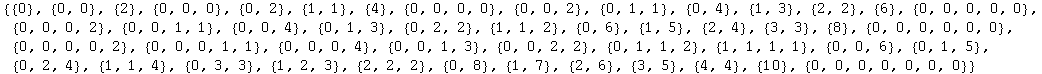
This function admits two additional arguments. The first specifies the order
In[52]:=
![InvarCases[8]](../HTMLFiles/InvarDoc.nb_217.gif)
Out[52]=
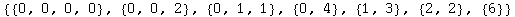
and the second specifies the degree
In[53]:=
![InvarCases[8, 3]](../HTMLFiles/InvarDoc.nb_219.gif)
Out[53]=
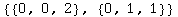

![[Graphics:../HTMLFiles/InvarDoc.nb_213.gif]](../HTMLFiles/InvarDoc.nb_213.gif)