8.2. Relation with our basis
The basis is given in terms of Weyl and Ricci. We need to convert the Weyl tensors into Riemann tensors, what takes quite a long time. The results form appendix B of the first paper.
Show timings over 1 second:
In[257]:=
![]()
The function do1 performs the translation from Weyl to Riemann (do1 has a very strange form in order to make it faster). The function do2 changes to invariants and simplify them:
In[258]:=
![]()
![]()
In[260]:=
![]()
Out[260]=
![]()
Pure Ricci:
In[261]:=
![]()
Out[261]=
![]()
In[262]:=
![]()
Out[262]=
![]()
In[263]:=
![]()
Out[263]=
![]()
In[264]:=
![]()
Out[264]=
![]()
Pure Weyl:
In[265]:=
![]()
Out[265]=
![]()
In[266]:=
![]()
![]()
Out[266]=
![]()
In[267]:=
![]()
Out[267]=
![]()
In[268]:=
![]()
![]()
Out[268]=
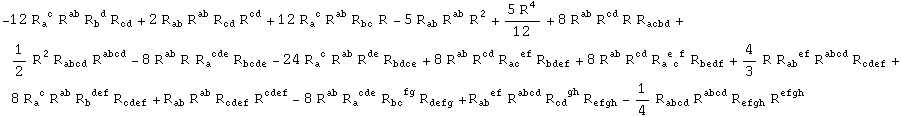
In[269]:=
![]()
Out[269]=
![]()
In[270]:=
![]()
![]()
Out[270]=
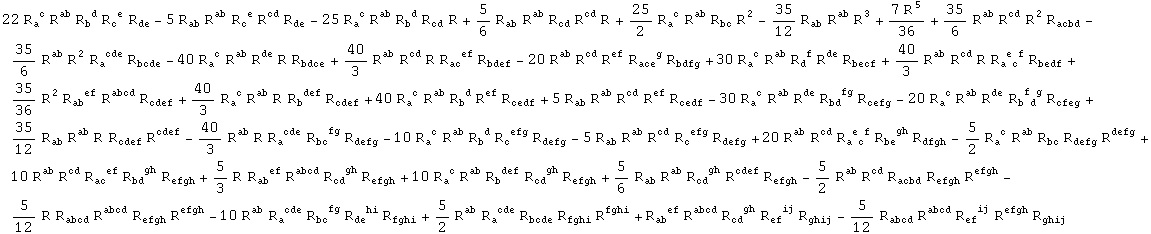
In[271]:=
![]()
Out[271]=
![]()
Mixed invariants:
In[272]:=
![]()
Out[272]=
![]()
In[273]:=
![]()
Out[273]=
![]()
In[274]:=
![]()
Out[274]=
![]()
In[275]:=
![]()
Out[275]=
![]()
In[276]:=
![]()
![]()
Out[276]=
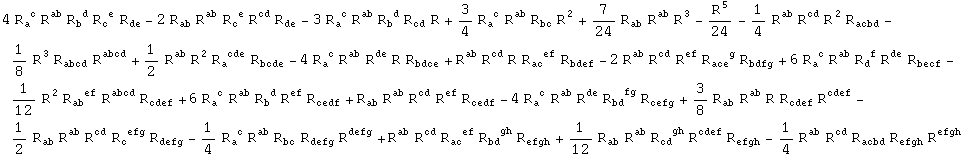
In[277]:=
![]()
Out[277]=
![]()
In[278]:=
![]()
Out[278]=
![]()
In[279]:=
![]()
Out[279]=
![]()
In[280]:=
![]()
Out[280]=
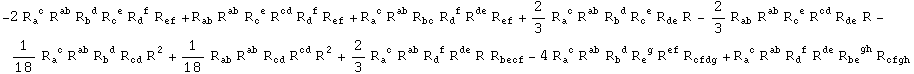
In[281]:=
![]()
Out[281]=
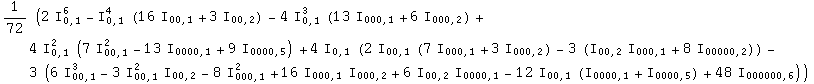
In[282]:=
![]()
![]()
Out[282]=
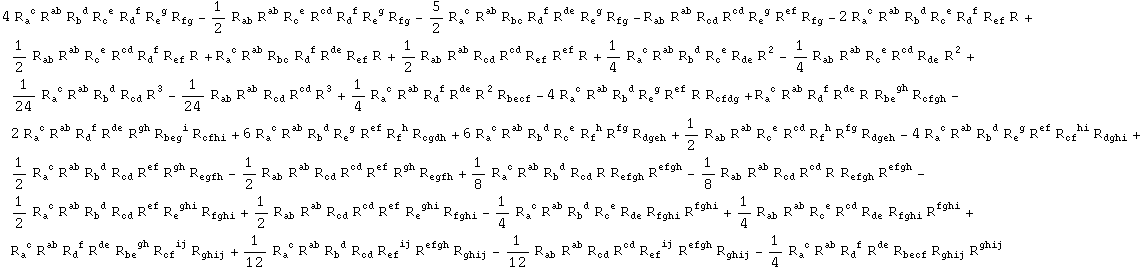
In[283]:=
![]()
![]()
Out[283]=
![]()
| Created by Mathematica (May 16, 2008) |