1. Example session
This is a simple example of the use of Invar`. The package is very easy to use: all its capabilities can be controlled through 10 basic commands. In addition, you will have to setup a basic xTensor` session, which we proceed to do now. We need to start by defining the manifold and metric of the Riemann tensor. For information on xTensor` see the file xTensorDoc.nb.
Define a 4d manifold M:
In[10]:=
![]()
![]()
![]()
Define a metric with negative determinant, with associated Levi-Civita connection CD:
In[11]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We included the option CurvatureRelations -> False so contractions of Riemanns will not be converted into Riccis. A number of tensors have been automatically defined. In particular there are the three curvature tensor fields
In[12]:=
![]()
Out[12]=
![]()
In[13]:=
![]()
Out[13]=
![]()
In[14]:=
![]()
Out[14]=
![]()
and their traceless counterparts:
In[15]:=
![]()
Out[15]=
![]()
In[16]:=
![]()
Out[16]=
![]()
with their expected trace properties:
In[17]:=
![]()
Out[17]=
![]()
In[18]:=
![]()
Out[18]=
![]()
The Riemann and Ricci tensors are not automatically replaced when they have contracted indices. Use ContractCurvature to do that:
In[19]:=
![]()
Out[19]=
![]()
In[20]:=
![]()
Out[20]=
![]()
In[21]:=
![]()
Out[21]=
![]()
In[22]:=
![]()
Out[22]=
![]()
We can change the output form of the tensors (note the use of Mathematica downvalues ^= )
In[23]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
So much for xTensor`. You will not need many more xTensor` functions to work with Invar`, but you will be able to do it more efficiently if you read the specific documentation for that package. Now we can start using the commands added by the package Invar`:
A typical algebraic Riemann scalar could be
In[30]:=
![]()
Out[30]=
![]()
which simplifies to
In[31]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[31]=
![]()
Notice how the different rules are read on the fly. We do not read them automatically because they would need several GB of memory. They are read only once (note the shorter timing now):
In[32]:=
![]()
Out[32]=
![]()
The head Scalar is introduced to avoid problems of index collisions.It can be removed using NoScalar:
In[33]:=
![]()
Out[33]=
![]()
We can generate random Riemann invariants using the command RandomRiemannMonomial, having as argument the case (see Section 2), in this example {0,4}, meaning one Riemann with no derivatives and another with a fourth derivative:
In[34]:=
![]()
Out[34]=
![]()
Any monomial can be canonicalized into one of a predefined list of canonical invariants. For the case {0,4} the list contains 126 canonical invariants, apart from the trivial canonical 0.
In[35]:=
![]()
Out[35]=
![]()
In particular, the previous object canonicalizes to
In[36]:=
![]()
Out[36]=
![]()
Many of the invariants actually do canonicalize to 0 so we iterate those two commands until we get something different from zero:
In[37]:=
![]()
![While[inv === 0, expr = RandomRiemannMonomial[{0, 4}]//NoScalar ; inv = RiemannToInv[expr] ; Print[ScreenDollarIndices[expr], " -> ", inv]] ;](../HTMLFiles/InvarDoc.nb_110.gif)
![]()
![]()
In[39]:=
![]()
Out[39]=
![]()
The canonical invariants can be expressed as a polynomial in a basis of indepent invariants, taking into account all the symmetries of the problem. This implies reading rules for additional `steps'
In[40]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[40]=
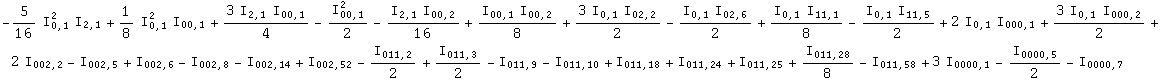
Finally this expression can be translated back into Riemann invariants.
In[41]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[41]=
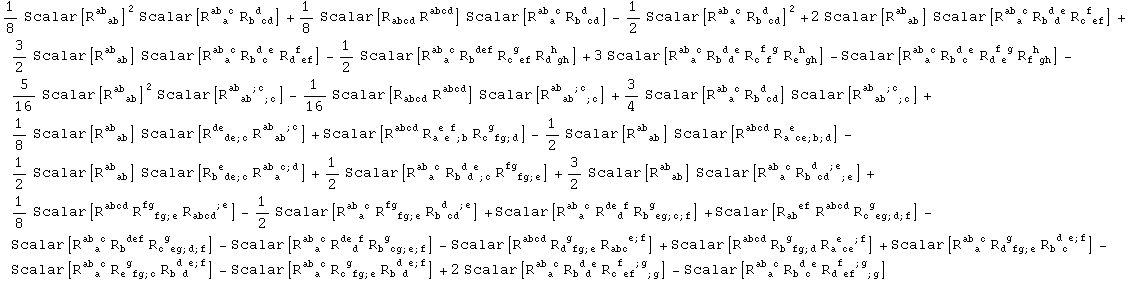
The whole process can be done in a single step using the command RiemannSimplify:
In[42]:=
![]()
Out[42]=
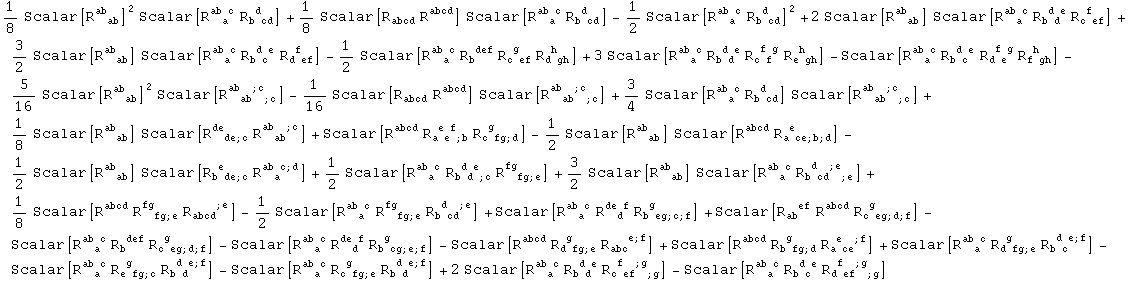
This is the example expression shown in the first paper:
In[43]:=
![]()
Out[43]=
![]()
In[44]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[44]=
![]()
And this is the example expression shown in the second paper:
In[45]:=
![]()
Out[45]=
![]()
In[46]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[46]=
![]()
| Created by Mathematica (May 16, 2008) |