6.4. Zero powers of Riemann
Surprisingly, there are monomials of the Riemann tensor which are zero due to the cyclic symmetry only. This first happens for a single monomial of degree 6:
It does not happen for degrees 1 to 5:
In[209]:=
![]()
Out[209]=
![]()
In[210]:=
![]()
Out[210]=
![]()
In[211]:=
![]()
Out[211]=
![]()
In[212]:=
![]()
Out[212]=
![]()
In[213]:=
![]()
Out[213]=
![]()
There is a single case in degree 6:
In[214]:=
![]()
Out[214]=
![]()
And 19 more cases for degree 7:
In[215]:=
![]()
Out[215]=
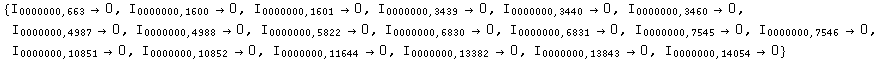
There is no obvious reason why this should be zero, and for all dimensions:
In[216]:=
![]()
Out[216]=
![]()
but we can check it in the pure Ricci case:
In[217]:=
![]()
Out[217]=
![]()
In[218]:=
![]()
Out[218]=
![]()
In[219]:=
![]()
Out[219]=
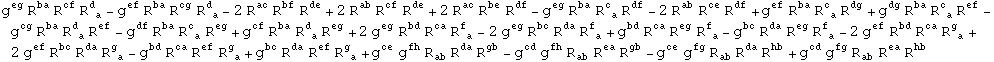
In[220]:=
![]()
Out[220]=
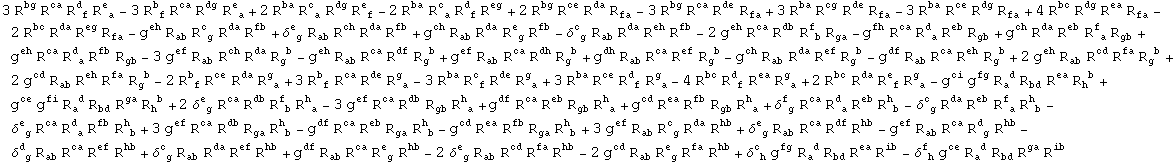
In[221]:=
![]()
Out[221]=
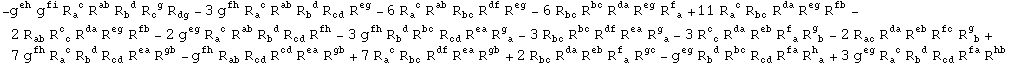
In[222]:=
![]()
Out[222]=
![]()
| Created by Mathematica (May 16, 2008) |