6.3. Tests
This is a collection of 54 examples, all of which must return 0.
First we add several indices:
In[131]:=
![]()
Shortcuts:
In[132]:=
![]()
![]()
Test of RiemannToInv and InvToRiemann:
In[134]:=
![]()
![]()
![]()
![]()
In[138]:=
![]()
![]()
![]()
![]()
![]()
Out[138]=
![]()
In[139]:=
![]()
Out[139]=
![]()
More tests of RiemannToInv, with algebraic invariants:
In[140]:=
![]()
![]()


In[144]:=
![]()
Out[144]=
![]()
In this case we need to guide the computation due to the products of epsilon tensors:
In[145]:=
![]()
In[146]:=
![]()
Out[146]=
![]()
Tests of RiemannSimplify:
In[147]:=
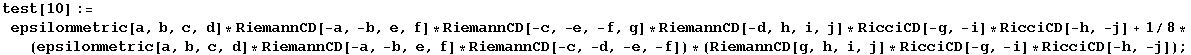
![]()
![]()

In[151]:=
![]()
Out[151]=
![]()
Tests of the cyclic symmetries:
In[152]:=
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
In[163]:=
![]()
In[164]:=
![]()
Out[164]=
![]()
In[165]:=
![]()
![]()
![]()
![]()
In[169]:=
![]()
![]()
![]()
Out[169]=
![]()
Tests of the Bianchi relations:
In[170]:=
![]()
![]()
![]()
![]()
In[174]:=
![]()
In[175]:=
![]()
![]()
![]()
Out[175]=
![]()
Tests of the commutation relations:
In[176]:=
![]()
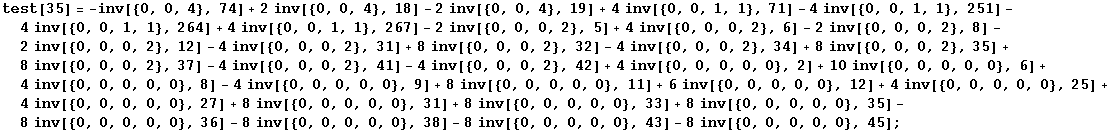
![]()
![]()
In[180]:=
![]()
In[181]:=
![]()
![]()
![]()
![]()
Out[181]=
![]()
Tests of the dimension dependent relations:
In[182]:=
![]()

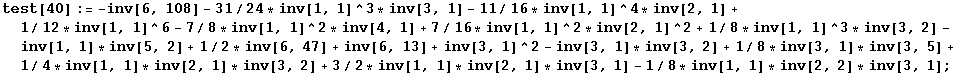
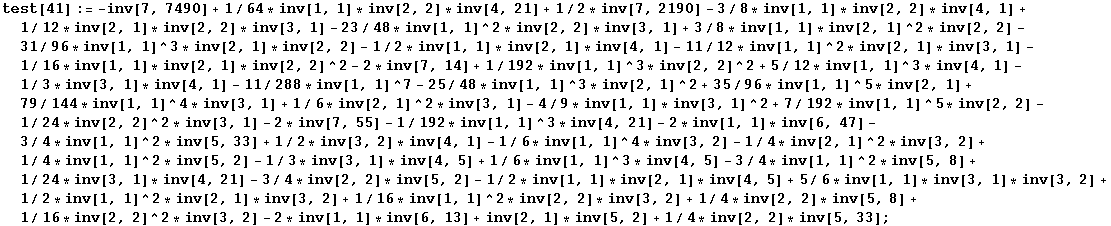
![]()
![]()
In[188]:=
![]()
In[189]:=
![]()
Out[189]=
![]()
In[190]:=
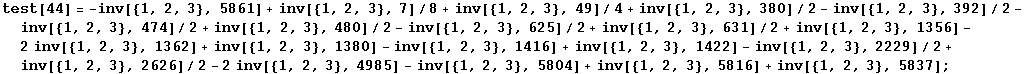
![]()
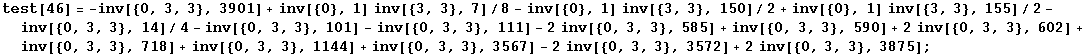
![]()
In[194]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[194]=
![]()
Test of the signature dependent relations:
In[195]:=
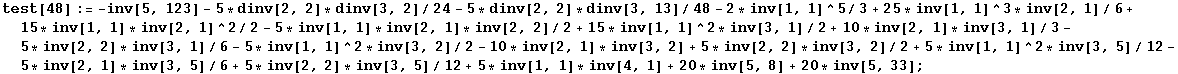
In[196]:=
![]()
In[197]:=
![]()
Out[197]=
![]()
In[198]:=

![]()


In[202]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[202]=
![]()
Test of WeylToRiemann:
In[203]:=

In[204]:=
![]()
Out[204]=
![]()
Test of ContractCurvature:
In[205]:=
![]()
In[206]:=
![]()
Out[206]=
![]()
Tidy up:
In[207]:=
![]()
![]()
| Created by Mathematica (May 16, 2008) |