6.1. InvSimplify

Once we have converted any Riemann expression into invariants with heads RInv and DualRInv, then we can "simplify" the expression by using the multiterm symmetries described above (steps 2, 3 and 4 of the simplification process). We use quotes because in many cases a single monomial is expanded into a large polynomial, its canonical form in the basis we have chosen, and this can be hardly called simplification. However, if an expression is equivalent to zero, the function InvSimplify will find it.

Example:

In[103]:=

Out[103]=

At level 1 nothing happens:

In[104]:=

Out[104]=

At level 2 the cyclic identity is used. Note that the degree does not change, but the indexes of the invariants decrease:

In[105]:=

Out[105]=

We skip levels 3 and 4 becasue there are no derivatives in this example. At level 5 we use dimensionally dependent identities for dimension 4:

In[106]:=

Out[106]=

At level 6 we use signature dependent identities expressing RInv[{0,0,0,0}, 21] in terms of DualRInv[{0,0}, 2] squared:

In[107]:=

Out[107]=

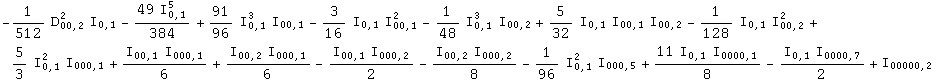
Another example, with derivatives and involving dual relations

In[108]:=

Out[108]=

In[109]:=

Out[109]=

In[110]:=

Out[110]=

In[111]:=

Out[111]=

In[112]:=

Out[112]=

In[113]:=

Out[113]=

Simplification of a dual invariant

In[114]:=

Out[114]=

In[115]:=

Out[115]=

In[116]:=

Out[116]=

In[117]:=

Out[117]=

By default, InvSimplify applies the first 6 steps. This behaviour can be changed with the following global variable

In[118]:=

Out[118]=

In[119]:=

Out[119]=

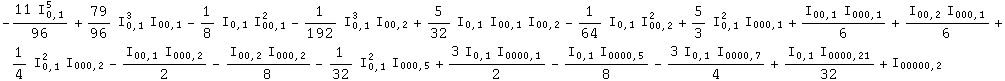
In[120]:=

Out[120]=

In[121]:=

Out[121]=

We return to the default value

In[122]:=

Out[122]=

Covariant derivatives commute when acting on scalars, which would in principle give an extra permutation symmetry. This symmetry is, however, not applied at step 1, but at step 4, along with the general rules for reordering of derivatives. For example, the following two invariants are obviously equal

In[123]:=

Out[123]=

In[124]:=

Out[124]=

Nevertheless, they are considered different objects until step 4

In[125]:=

Out[125]=

In[126]:=

Out[126]=

Created by Mathematica  (May 16, 2008)